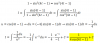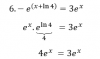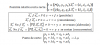-
Christian Buele
el 23/11/16 -
Gregory
el 23/11/16 -
Juan
el 23/11/16Tengo los siguientes datos:
recta s: y= x+k
circunferencia c: x2+y2+2x-3=0
He obtenido que el centro de la equación = (-1 , 3/2)
I el radio = 1,8
La pregunta me pide que si la recta s es tangente a c
d(O,s)=
0. 2r, >r, r
Luego tengo que desarollar la siguiente ecuación adaptada y encontrar los valores K:
Antonius Benedictus
el 23/11/16
Juan
el 23/11/16
Antonius Benedictus
el 23/11/16 -
Carlos Ojeda
el 23/11/16Hola, si me diesen las ecuaciones implícitas de un subespacio y fuesen de este tipo:
a+b +c +d = 0
2a+5b-3c+5d = 0
3a-6b+2c-d = 0
¿Cómo harían para hallar las ecuaciones paramétricas a partir de las implícitas? Gracias
-
Carlos Ojeda
el 23/11/16
Hola, Pido ayuda a los profesores Antonio Benito y César, si me pidiesen demostrar que v= { (1,2,4,6) ∈ M2 (R) } es un subespacio vectorial (utilizando las tres propiedades), ¿cómo lo harían? cuando me lo dan en forma de matriz (a b / c d) sé demostrarlo pero si es un vector, me lío. El vector (1,2,4,6) me lo inventé, si no es demostrable, pongan uno que se pueda demostrar. Gracias!
David
el 25/11/16Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
Axel Morales Piñón.
el 23/11/16Buenas días ... he metido la patita ¿¿??
-
Lola Melola
el 23/11/16No es una pregunta ni nada, pero me alegra ver como la gente puede ser capaz de ayudarse mutuamente a través de este foro :) Todos necesitamos alguna vez de Unicoos y es increíble lo mucho que ha crecido esta plataforma desde que la conoci por allá en 2013 :) Espero que les pueda ir bien a todos en sus ejercicios :) Un saludo
-
daniel
el 23/11/16 -
Gabriel
el 23/11/16Si por ejemplo necesito obtener un punto de una "interseccion" de dos rectas.Me dan las dos ecuaciones de las rectas en forma continua. Esta bien si procedo asi?
.Priemero llevo ambas ecuaciones a la forma implicita.Me quedaria un sistema de 4 ecuaciones.De ahi, le doy un valor arbitrario a una de las incognitas..y calculo los dos puntos restantes.
El P(x,y,z) obtenido de esa manera, me sirve como punto de esa interseccion? o lo estoy haciendo mal?
-
Mariam
el 23/11/16Porfa, si me pueden ayudar se los agradecería, mañana tengo examen :C
Antonio Silvio Palmitano
el 23/11/1618) Tienes información en el enunciado del problema:
f ' ' (x) ≠ 0 en el intervalo I
f(x) > 0 en el intervalo I, ya que la función es positiva
f ' ' (x) > 0 en el intervalo I, ya que la función es cóncava hacia arriba.
Luego, piden estudiar la concavidad de la función compuesta cuya expresión es:
g(x) = ( f(x) )2, planteamos su derivada primera (observa que debemos aplicar la Regla de la Cadena):
g ' (x) = 2f(x) * f ' (x), planteamos su derivada segunda (observa que debemos aplicar la regla para un producto):
g ' ' (x) = 2f ' (x) * f ' (x) + 2f(x) * f ' ' (x), reducimos factores en el primer término y queda:
g ' ' (x) = 2( f ' (x) )2 + 2f(x) * f ' ' (x) > 0, por lo que tenemos que la función g es cóncava hacia arriba (observa que los dos términos de la expresión son positivos, porque son productos de factores positivos).
Espero haberte ayudado.
