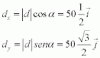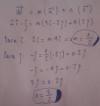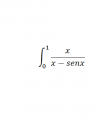Foro de preguntas y respuestas de Matemáticas

Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.

Ir a beUnicoos

DueFreitas
el 22/11/16

Profe este ejercicio me cuesta

••0 voto/s
•
César
el 22/11/16
Va Due

•0 voto/s
•

Cancelar
Manu
el 22/11/16

Buenos días.
Algún unicoos que me diga de donde salen las fracciones, por favor.
gracias.

••0 voto/s
•
César
el 22/11/16
Es un error están al reves sen y cos

•1 voto/s
•

Cancelar
Manu
el 22/11/16

Buenos días..
Calcular m y n para que se verifique w = m u + n v, siendo u = 4i - 8j , v = 2j , w = 2i - j
dice que m = 1/2 y n = 3/2 pero no se desarrollarlo.

••0 voto/s
•
Ángel
el 22/11/16

•1 voto/s
•

Cancelar
carmela
el 22/11/16

Buenos días. Este ejercicio está sacado del material adicional de su página. En la matriz, el término independiente final es correcto?

••0 voto/s
•
César
el 22/11/16
Te lo dejo por Gauss

•1 voto/s
•
carmela
el 22/11/16
Muchas gracias César

•0 voto/s
•

Cancelar
Mario
el 22/11/16

Alguien me aydua a decir si coverge o diverge?? Lo intente comprandola con 1/x pero se me complica un poco no me da muchos resultados.

••0 voto/s
•
David
el 25/11/16
Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas

Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)

Por si te ayuda, grabé varios vídeos de INTEGRALES IMPROPIAS como excepción... Integrales Impropias

•0 voto/s
•

Cancelar
Manu
el 22/11/16

Buenos días.
Dice:
Dados los vectores a= 2i + 4j + 6k y b= i -2j + 3k
a) el vector de suma s= a + b = (2i + 4j + 6k) + (i -2j + 3k) = (3 , 2 , 9)
b) |s| = √94 ¿de donde sale la raíz de 94?
c) dice: el vector de diferencia d = a - b = (1 , 6 , 3) Entiendo el cambio de signos y el resultado pero no el por que de la (d) y no usar la (c) de d =a - b. ¿hay algo que me pierdo o es insignificante?
Y este otro dice que d u_d = ( 1/√46 , 6/√46 , 3/√46) entonces entiendo que utilizo para el numerador los números de ejercicio c donde d = a - b pero ¿de donde sale la raíz de 46?
Gracias.

••0 voto/s
•
Ángel
el 22/11/16
s=(3 , 2 , 9)
|s| = √(3²+2²+9²)
|s| = √94

Lo de llamar "d" es insignificante, lo llaman d por diferencia...pero podrías haberle llamado c,m,n,h....o Pepito incluso :D

d=(1, 6, 3)
|d| = √1²+6²+3²)
|d| = √46
Como U_d= d/|d|, entonces U_d= ( 1/√46 , 6/√46 , 3/√46)

•1 voto/s
•

Cancelar
Manu
el 22/11/16

Buenos días.
Vectores:
c= 2a - 3b= 2·(3i - 2j) - 3(-4i + j) = (6i - 4j) + (12 - 3)= (18, -7)
Luego para el ejercicio siguiente dice que es un vector unitario del vector c (U_c)
c (U_c) = U_c = ( 18/√ 373 , - 7/√ 373 ) y es que, no se de donde sacan √ 373 ni el signo tampoco. Ya he visto todos los vídeos y los he hecho.
Si algún unicoos puede ayudarme, gracias.

••0 voto/s
•
Ángel
el 22/11/16
c=(18, -7)
|c| = √182+(-7)2
|c| = √373
Como Uc= c/|c|, entonces Uc = ( 18/√ 373 , - 7/√ 373 )

•1 voto/s
•

Cancelar
Nicolás
el 22/11/16

Buenos días.
Tengo la integral de (4x^2)/(1-8x^3)^4 dx Me piden que resuelva por método de sustitución.

••0 voto/s
•
Antonius Benedictus
el 22/11/16
Haz el cambio:
t=1-8x³
dt=-24x²dx
4x² dx=-(1/6) dt
Entonces:
∫(-1/6)dt/t =(-1/6)ln(abs(t))+C=(-1/6)ln(abs(1-8x³)) +C

•1 voto/s
•

Cancelar
Manu
el 22/11/16

Buenos días.
En el ejercicio c entiendo que multiplico el 3 por el número de recuadros que abarca la flecha a,, siendo (18,0) y 0 por que no pide b.
En el ejercicio d entiendo que multiplico 3 por los recuadros que abarca la flecha hasta el recuadro donde empieza b siendo 3·4=12 y para b 2 por el número de recuadros que abarca b siendo -2·5=-10
Ahora, para los ejercicio a y b por esta norma no los entiendo.
Si algún unicoos puede ayudarme, por favor. Gracias.

••0 voto/s
•
David
el 22/11/16
El vector b = (3,5). El vector a=(6,0)...
...... 3a=3.(6,0)=(18,0)

•1 voto/s
•

Cancelar
daniel
el 22/11/16

∫1+cos4Θ /2 dΘ

••0 voto/s
•
Antonio Silvio Palmitano
el 22/11/16
Si la integral está expresada:
I = ∫ ( 1 + cos4Θ )/2 * dΘ, extraemos el factor constante y queda:
I = (1/2) ∫ ( 1 + cos4Θ ) * dΘ, luego planteamos la sustitución (cambio de variable:
w = 4Θ, de donde tienes: dw = 4dΘ, y puedes despejar: (1/4)dw = dΘ, luego sustituyes y qued:
I = (1/2) ∫ ( 1 + cosw ) * (1/4)dw, luego extraemos factor constante y queda:
I = (1/8) ∫ ( 1 + cosw ) dw, integramos y queda:
I = (1/8) ( w + senw ) + C, luego volvemos a sustituir para recuperar la variable original y queda:
I = (1/8) ( 4Θ + sen(4Θ) ) + C, distribuimos y llegamos a:
I = (1/2)Θ + (1/8)sen(4Θ) + C.
Espero haberte ayudado.

•0 voto/s
•

Cancelar