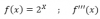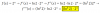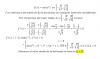-
Lorena Llanos
el 23/11/16Hola,
Su ayuda con esta derivada de orden superior
Mil gracias
Antonio Silvio Palmitano
el 23/11/16Observa que tienes la expresión de una función exponencial de base 2:
f(x) = 2x, luego planteamos su derivada primera:
f ' (x) = 2x * ln2, luego plantamos su derivada segunda (observa que el segundo factor es constante):
f ' ' (x) = 2x * ln2 * ln2 = 2x * (ln2)2,
luego plantamos su derivada tercera (observa que el segundo factor es constante):
f ' ' ' (x) = 2x * ln2 * (ln2)2 = 2x * (ln2)3.
Espero haberte ayudado.
-
Mariam
el 23/11/16Me ayudarían porfa?
Antonio Silvio Palmitano
el 23/11/16Comencemos por plantear el incremento de la función para x = 0:
f(0+h) - f(0) = f(h) - f(0) = e^(-1/h2) - 0 = e^(-1/h2)
Luego pasamos al cociente incremental:
( f(0+h) - f(0) ) / h = e^(-1/h2) / h
Luego pasamos al límite del cociente incremental, para el incremento tendiendo a cero:
f ' (0) = Lím(h->0) e^(-1/h2) / h =
planteamos la sustitucón: w = 1/h2 (observa que w tiende a +infinito cuando h tiende a cero):
= Lím(w->+inf) e-w / (1/√(w)) =
operamos en el argumento y queda:
= Lím(w->+inf) √(w)/ew= 0,
ya que √(w) es mucho menor que ew cuando w tiende a +infinito (observa que también puedes llegar al resultado aplicando la Regla de L'Hôpital).
Espero haberte ayudado
-
Alexis de Barros
el 23/11/16 -
Martín Ramírez
el 23/11/16Hola, necesito una ayudita con el siguiente ejercicio:
Considere la función f(x) = Cos(x2) definida en el intervalo [-√(π/3) ; √(π/3)].
Determine un punto c ∈ ]-√(π/3) ; √(π/3)[ tal que la recta tangente en (c , f(c)) sea paralela a la recta que une los puntos P(-√(π/3) , 1/2) y Q(√(π/3) , 1/2).
Gracias de antemano.
Antonio Silvio Palmitano
el 23/11/16Observa que tienes:
Hipótesis 1: D = [-√(π/3) ; √(π/3)] es un intervalo cerrado.
Hipótesis 2: f(x) = cos(x2) es la expresión de una función continua en D (observa que es composición de funciones continuas)
Hipótesis 3: f( -√(π/3) ) = f( √(π/3) ) = 1/2.
Luego, por el Teorema de Rolle, tienes que existe c ∈ D tal que f ' (c) = 0.
Luego, la recta tangente a la gráfica de la función en el punto de coordenadas (c, f(c)) es igual a 0, y observa que la pendiente de la recta que une los extremos del intervalo es:
m = (1/2 - 1/2) / ( √(π/3) - (-√(π/3)) ) = 0 / 2V(3) = 0,
por lo que concluimos que las dos rectas son paralelas, ya que tienen pendientes iguales.
Espero haberte ayudado.
-
Raisa
el 23/11/16Hola Unicoos,
¿Cuál es la inversa de la siguiente función?
Gracias!
Antonio Silvio Palmitano
el 23/11/16Observa que el dominio de la función f(x) = 2x, (observa que el enunciado indica: x >0) es el intervalo: D = (0,+inf) y, como se trata de una función exponencial, su imagen es el intervalo: I = (0,+inf), como ocurre con todas las funciones exponenciales.
Luego, la función inversa: f-1(x) tendrá dominio: Di = (0,+inf) = I, e imagen: Ii = (0,+inf) = D, y su expresión será:
f-1(x) = log2x.
Recuerda la definición de logaritmo en base 2:
log2x = y ⇔ x = 2y.
Espero haberte ayudado.
-
Raul Flow
el 23/11/16
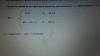
Buenas noches unicoos. En primer lugar agradeceros los tutoriales y la ayuda por redes sociales. Me ha venido genial aprender con vosotros para mi asignatura de mates de primero de grado, sobre todo los videos de youtube, en los que el profe es simplemente genial.Mi duda os la dejo en dos imágenes. Estoy con una integral irracional, con dos cambios de variable. El primero es "X = sec t" y en el segundo realizo otro cambio de variable de "u = sin t". La resolución en si de la integral no me crea dudas, pero el problema viene cuando consigo una integral racional del tipo (1+u)(1-u) en el denominador. Calculo los numeradores A y B como explica Daniel en youtube y me sale 1/2 para A y 1/2 para B. Con ello llego a una suma de logaritmos neperianos, pero el problema esta en que en los ejercicios resueltos por el profesor nos aparece una resta de logaritmos neperianos y por tanto debe ser el logaritmo de una división, no de un producto como me sale a mi. Os dejo una image y agradecería me indicarais en que punto fallo.
Muchisimas gracias por vuestra ayuda. A ver si apruebo el viernes !!!!!
David
el 25/11/16Tienes esa misma integral en un video.. Integral TRIGONOMETRICA con cambio de variable SECANTE
P.D. Me llamo David #nosvemosenclase
-
Armando Buele
el 22/11/16 -
Christian Plasencia
el 22/11/16Hola, que tal amigos.
Por favor me podrían ayudar con este ejercicio?
Mil gracias muy amables.
-
carmen ruiz
el 22/11/16 -
elkyn zambrano
el 22/11/16
