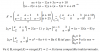-
Hola buen día, tengo un ejercicio: Encuentre la ecuación de la recta tangente en (1,1) de la función y= x^2-2x+2, y segun mi resultado me da que y= 1, quisiera saber si estoy bien por favor, gracias.


Antonio Silvio Palmitano
el 19/11/16Si, es correcta tu respuesta: la ecuación de la recta tangente a la gráfica en el punto de coordenadas V(1,1) tiene ecuación y = 1.
Observa que la gráfica de la función es una parábola con vértice en el punto indicado, y con eje de simetría paralelo al eje OY. Da aquí es que la recta tangente es paralela al eje OX.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 19/11/16Para el ejercicio (a). Proponemos un contraejemplo con dos funciones partidas:
f(x) =
1 si x ≥ 0
-1 si x < 0
observa que el dominio de la función es: Df = R, y que es discontinua esencial en x = 0.
g(x) =
2 si x ≥ 0
4 si x < 0
observa que el dominio de la función es Dg = R, y que es discontinua esencial en x = 0.
Luego, planteamos la expresión de la función suma:
su dominio será: Df+g = Df ∩ Dg = R, queda:
(f+g)(x) = f(x) + g(x) =
1 + 2 si x ≥ 0
-1 + 4 si x < 0
Luego, finalmente la expresión de la función suma de f con g queda:
(f+g)(x) =
3 si x ≥ 0
3 si x < 0
y observa que es una función continua en todo su dominio.
Espero haberte ayudado.
-
Antonio Benito, me preguntaba si podrías ayudarme en este ejercicio. Gracias de antemano. Saludos cordiales.
Simplifica:


Antonio Silvio Palmitano
el 19/11/16Una forma alternativa podría ser (si has visto este tema en clase), expresar a todas las raíces, distribuidas entre los factores de sus argumentos, como potencias con exponente fraccionario (recuerda que quedan en la forma up/r, donde p es el exponente de la potencia, y r es el índice de la raíz correspondiente).
Luego, expresamos las raíces de la expresión como potencias con exponente fraccionario:
el numerador (N) y el denominador (D) quedan:
N = a1/6b1/6 * a2/3b4/3 * b5/2 = a1/6+2/3b1/6+4/3+5/2 = a5/6b4 = a5/6b24/6;
D = a2/4b3/4.
Luego pasamos a la expresión fraccionaria:
N/D = a5/6b24/6 / a2/4b3/4 = a5/6-2/4b24/6-3/4 = a4/12b39/12 = a4/12b3+3/12 = a4/12b3 b3/12 = b3(a4b3)1/12.
Luego, observa que la última expresión se corresponde con la última expresión en el desarrollo del colega Antonio.
Observa que en toda la tarea, luego de expresar a las raíces como potencias con exponentes fraccionarios, hemos aplicado propiedades del producto y de la división de potencias con bases iguales, y hemos tratado de expresar los exponentes como fracciones con el mismo denominador común para todas.
Espero haberte ayudado.
-
Buenas unicoos, tengo un problema sobre vectores en el espacio que no se resolver, alguien me puede ayudar?
·Sean dos vectores a→ y b→ que cumplen las siguientes condiciones:
- a) Módulo de a→ = Módulo de b→ = 4
- b)El ángulo que forman a→ y b→ es de 30º
Calcula el área del triángulo construido sobre los siguientes vectores:
a→ -2b→ y 3a→ +2b→
Muchas gracias!!


Antonio Silvio Palmitano
el 19/11/16Recuerda algunas propiedades del producto vectorial:
1) | u x v | = |u|*|v|*senα, donde α es el ángulo formado por los vectores u y v (observa que | u x u | = 0, ya que u x u = N (vector nulo)).
2) | u x v | = Área del paralelogramo determinado por los vectores u y v.
3) | u x v | / 2 = Área del triángulo determinado por los vectores u y v.
4) El producto vectorial es distributivo con respecto a la suma y a la resta de vectores.
5) El producto vectorial no es conmutativo: u x v = - v x u.
6) Producto vectorial por escalar: ku x v = u x kv = k(uxv).
Luego, observa que te piden calcular el área del triángulo determinado por los vectores:
u = a-2b, y v = 3a+2b,
Con los ojos puestos en la propiedad 3, planteamos el producto vectorial:
u x v = (a -2b)x(3a + 2b) = distribuimos (propiedad 4) y queda:
u x v = a x 3a + ax2b - 2bxa - 4bxb = extraemos factores escalares en los términos (propiedad 6) y queda:
u x v = 3(a x a) + 2(a x b) - 2(b x a) - 4(b x b) = observa que el primero y el cuarto término son nulos (propiedad 1) y queda:
u x v = 3N + 2(a x b) - 2(b x a) - 4N = resolvemos el primero y el cuarto término y queda:
u x v = N + 2(a x b) - 2(b x a) - N = cancelamos los términos nulos y queda:
u x v = 2(a x b) - 2(b x a) = aplicamos la propiedad 5 en el tercer término (observa que cambia de signo) y queda:
u x v = 2(a x b) + 2(a x b) = reducimos términos semejantes y queda:
u x v = 4(a x b).
Luego, según la propiedad 3, pasamos al cálculo del área del triángulo determinado por los vectores u y v:
ATr = | u x v | = | 4(a x b) | = 4*| a x b | = aplicamos la propiedad 1 y queda:
ATr = 4*| a| * | b | * senα = 4*4*4*sen30° = 4*4*4*1/2 = 32.
Espero haberte ayudado.
-
Otro problema unicoos:
Sea T un endomorfismo de R^n:
a) Si e, e' son vectores independientes tales que e es un vector propio de valor α i e' es un vector propio de valor β, los dos respecto a T, ¿qué condición se tiene que cumplir para que e + e' también sea un vector propio de T? ¿Con qué valor?
b) Explica qué simetrías axiales del plano admiten vectores propios no nulos. Indica el valor de cada vector.
Muchas gracias!!


David
el 21/11/16Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)