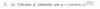-
Buenas unicoos!! No sé como resolver este problema:
Encuentra y clasifica la única isometría directa de R3 que cumple T(1,2,2)=(2,1,2) y T(2,1,0)=(0,2,1).


David
el 21/11/16Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
Hola, tengo este problema y no estoy seguro de responder bien. "Encuentra todos los valores que puede tener la última cifra de un cuadrado perfecto". ¿Me pueden ayudar? Gracias.


Antonio Silvio Palmitano
el 19/11/16Consideremos un número natural cualquiera, por ejemplo: N = 25
Puedes escribirlo: N = 20 + 5, y lo mismo ocurre en general:
al presentar la última cifra en un término aparte, cualquier número natural x queda expresado como la suma de un múltiplo de 10 más una cifra.
Tenemos entonces para un número natural x:
x = 10a + c, con a ∈ N, c ∈ N y 0 ≤ c ≤ 9.
Luego planteamos su cuadrado:
x2 = (10a + c)2, desarrollamos y queda:
x2 = 100a2 + 20ac + c2, extraemos factor común 10 en los dos primeros términos y queda:
x2 = 10(10a2 + 2ac) + c2,
observa que el primer término de la derecha corresponde a un múltiplo de 10, por lo que su última cifra es cero,
y observa también que la última cifra del número natural x2 la aportará el término c2, por lo tanto,
pasamos a estudiar los posibles valores de c2:
02 = 0,
12 = 1,
22 = 4,
32 = 9,
42 = 16 = 10 + 6,
52 = 25 = 20 + 5,
62 = 36 = 30 + 6,
72 = 49 = 40 + 9,
82 = 64 = 60 + 4,
92 = 81 = 80 + 1.
Por lo tanto, para el cuadrado de un número natural, su última cifra será:
0, si la última cifra del número es 0,
1, si la última cifra del número es 1 o 9,
4, si la última cifra del número es 2 u 8,
5, si la última cifra del número es 5,
6, si la última cifra del número es 4 o 6,
9, si la última cifra del número es 3 o 7.
Observa que no hay números naturales tales que sus cuadrados tengan última cifra 2, 3, 7 u 8.
Espero haberte ayudado.
-
Hola. Tenia esta duda.
Encuentra la ecuacion diferencial cuya solucion sea:
a) y=x2+C
yo lo que hice fue derivar y me quedo y`=2x y mi duda es si la ecuacion diferencial es : y`-2x=0 ????, mi duda es q la constante desaparecio y cuando resolvia otros ejercicios la constante no se iva....
b) Este ejercicio no sabia como hacerlo...
y=A cosx
Dejo una imagen como lo hace mi profesor....


Antonio Silvio Palmitano
el 19/11/16a) Lo has resuelto correctamente. Tienes la ecuación:
y = x2 + C.
Observa que en tu apunte te indican despejar la constante, lo haces y queda:
y - x2 = C, luego derivas término a término y queda:
y ' - 2x = 0, luego haces pasaje de término y queda:
y ' = 2x.
b) Tienes la ecuación:
y = Acosx.
Despejas la constante y queda:
y / cosx = A, luego derivas en ambos miembros (observa que en el primero debes aplicar la regla del cociente):
(y ' * cosx + y * senx) / cos2x = 0, haces pasaje de divisor como factor, resuelves el segundo miembro y queda:
y ' * cosx + y * senx = 0, haces pasaje de término y queda:
y ' * cosx = - y * senx, haces pasajde de factor como divisor y queda:
y ' = - y * senx/cosx, aplicas la identidad trigonométrica de la tangente y queda:
y ' = y * tanx.
Observa que si en la ecuación inicial tienes una sola constante arbitraria, tienes una ecuación diferencial de primer orden, en cuya expresión intervienen y, y ' y una función de x.
Espero haberte ayudado.
-
Me pueden ayudar con esta ecuacion trigonométrica
Seno²(theta)+2seno(theta)cos(theta) - coseno²(theta) =0


Antonio Silvio Palmitano
el 19/11/16Partimos de la ecuación trigonométrica:
sen2Θ + 2senΘcosΘ - cos2Θ = 0, haces pasaje de términos y queda:
2senΘcosΘ = cos2Θ - sen2Θ,
observa que tienes las expresiones correspondientes a identidades trigonométricas del doble de un ángulo en ambos miembros:
sen(2θ) = cos(2Θ), haces pasaje de factor como divisor y queda:
sen(2θ) / cos(2Θ) = 1, aplicas la identidad trigonométrica de la tangente y queda:
tan(2θ) = 1, que nos conduce a dos opciones, una en el primer cuadrante y otra en el tercer cuadrante:
a) 2Θ = 45°, y en general:
2Θ = 45° + 360°*k, con k ∈ Z, luego dividimos pos 2 en todos los términos de la ecuación y queda:
Θ = 22,5° + 180°*k, con k ∈ Z.
b) 2Θ = 225°, y en general:
2Θ = 225° + 360°*k, con k ∈ Z, luego dividimos pos 2 en todos los términos de la ecuación y queda:
Θ = 112,5° + 180°*k, con k ∈ Z.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 19/11/16Recordemos la definición de cologaritmo:
cologbx = logb(1/x), luego aplicamos la propiedad del logaritmo de una división:
cologbx = logb1 - logbx, luego resolvemos el primer término en el segundo miembro:
cologbx = 0 - logbx, luego cancelamos el término nulo:
cologbx = - logbx.
Vamos al ejercicio:
log3(5x - 1) + colog3(3x - 5) = 2, sustituimos el segundo término del primer miembro según la ecuación remarcada:
log3(5x - 1) - log3(3x - 5) = 2, aplicamos la propiedad del logaritmo de una división:
log3( (5x - 1) / (3x - 5) ) = 2, componemos con la función inversa del logaritmo en base 3:
(5x - 1) / (3x - 5) = 32. resolvemos el segundo miembro y hacemos pasaje de divisor como factor:
5x - 1 = 9(3x - 5), distribuimos en el segundo miembro:
5x - 1 = 27x - 45, hacemos pasajes de términos, reducimos términos semejantes y queda:
- 22x = - 44, dividimos en ambos miembros por -22 y queda:
x = 2.
Puedes verificar que la solución es válida reemplazando en la ecuación inicial.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 19/11/16Has presentado bien las dos opciones que tienes a partir de la inecuación con valor absoluto.
Como no conoces el valor de x, el valor c que interviene en la expresión del resto será:
a) c comprendido entre 0 y x, si x es positivo: 0 ≤ c ≤ x, si x ∈ (0 , 0,25);
b) c comprendido entre x y 0, si x es negativo: x ≤ c ≤ 0,25, si x ∈ (-0,25 , 0).
Observa que para estima el resto en valor absoluto, en ambos casos acotas; |c| ≤ |x| ≤ 0,25.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 19/11/16Va una orientación.
Observa que la expresión es una potencia, cuya base es una función, y cuyo exponente es otra función.
En general, llamamos u a la base, v al exponente y la expresión general queda:
y = uv, luego, escribimos a la base como una expresión exponencial:
y = ( elnu )v, luego aplicamos la propiedad de la potencia cuya base es otra potencia:
y = elnu*v, luego pasamos a la derivada (observa que debemos aplicar la regla de la cadena):
y ' = elnu*v * ( (1/u) * u ' * v + lnu * v ´ ), observa que en el primer factor tenemos la expresión remarcada, sustituimos y queda:
y ' = uv * ( (1/u) * u ' *v + lnu * v ´ ).
Luego, puedes guardar esta expresión para aplicarla en casos como el que consultas. Observa que en tu ejercicio tienes:
u = arcsenx, cuya derivada queda: u ' = 1/√(1 - x2)
v = senx/(1 + x2), cuya derivada queda: v ' = ( cosx * (1 + x2) - senx * 2x ) / (1 + x2)2.
Luego, solo queda que sustituyas las cuatro expresiones en la expresión remarcada de la derivada de la función.
Espero haberte ayudado.
-
Muy buenas tardes :D agradeceria me ayudaran
La resistencia de una viga rectangular es proporcional al producto del ancho por el cubo del espesor.Calcular las dimensiones de la viga mas resistente que puede cortarse de un tronco cilindrico de radio a.
PD: Le he estado dando vueltas pero la lio xD, gracias de antemano :)


Antonio Silvio Palmitano
el 18/11/16Planteamos para la resistencia de la viga: R(A,e) = k*A*e3 , k es una constante de proporcionalidad.
Luego, como la pieza de material es cilíndrica (no es rectangular), planteamos la relación entre el ancho y el espesor de la viga que se debe tallar. Para ello, dibuja una circunferencia con centro en el origen y radio a (su ecuación es: x2 + y2 = a2), y en ella dibuja un rectángulo con base sobre el eje OX y vértices sobre la circunferencia cuyas coordenadas son P(x,y), Q(-x,y). Lo haces, y verás:
base del rectángulo = ancho de la viga = A = 2x (*);
altura del rectángulo = espesor de la viga = e = y = V(a2 - x2) = (a2 - x2)1/2 (**).
Luego, sustituimos en la expresión remarcada, y tenemos para la resistencia de la viga:
R(x) = k*2x*( (a2 - x2)1/2 )3 ), resolvemos exponentes y queda:
R(x) = k*2x*(a2 - x2)3/2 .
Luego, planteamos la expresión de la derivada primera, e igualamos a cero para buscar puntos críticos:
R ' (x) = 2k*(a2 - x2)3/2 - 6kx2(a2 - x2)1/2, luego planteamos:
2k*(a2 - x2)3/2 - 6kx2(a2 - x2)1/2 = 0, hacemos pasaje de término:
2k*(a2 - x2)3/2 = 6kx2(a2 - x2)1/2, dividimos en ambos miembros por 2k y queda:
(a2 - x2)3/2 = 3x2(a2 - x2)1/2 , hacemos pasaje de factor como divisor, y queda:
(a2 - x2)3/2 / (a2 - x2)1/2 = 3x2, simplificamos en el primer miembro y queda:
a2 - x2 = 3x2, hacemos pasajes de términos, reducimos términos semejantes y queda:
- 4x2= - a2, multiplicamos en ambos miembros por - 1/4 y queda:
x2= a2/4, luego hacemos pasaje de potencia como raíz, y llegamos a:
x = a/2 (queda para que verifiques que corresponde a un máximo).
Luego, reemplazamos en las expresiones del ancho y del espesor señaladas (*) (**) y quedan:
A = 2*a/2 = a.
e = ( a2 - a2/4 )1/2 = ( 3a2/4)1/2 = (√(3)/2)a.
Espero haberte ayudado.
-
Buenas tardes, tengo un duda con el siguiente ejercicio:
Determine el vertice una parábola que pasa por los puntos (1,3) y (5,6).Solo me dan esos datos no tengo idea de como hacerlo ya que no me dan ni P o el foco de la parábola.


Antonio Silvio Palmitano
el 18/11/16Primero que todo, debes verificar que el enunciado esté completo.
Y si es así, existen infinitas parábolas, que pueden tener eje de simetría paralelo a uno u otro de los ejes coordenados, o tener ejes no paralelos a ellos.
Vamos con el caso de eje de simetría paralelo a OY. Llamamos V(h,k) al vértice que buscamos, y planteamos la ecuación canónica:
(x - h)2 = 4c(y - k)
Luego, como el punto de coordenadas A(1,3) pertenece a la parábola, reemplazamos y queda: (1 - h)2 = 4c(3 - k) (*),
y como el puntos de coordenadas B(5,6) también pertenece a la parábola, reemplazamos y queda: (5 - h)2 = 4c(6 - k) (**).
Luego, tenemos el sistema de dos ecuaciones señaladas (*) (**) con tres incógnitas:
(1 - h)2 = 4c(3 - k)
(5 - h)2 = 4c(6 - k)
Si te piden "hallar el vértice de una parábola", puedes elegir un valor no nulo para c, por ejemplo c = 1, y el sistema queda:
(1 - h)2 = 4(3 - k)
(5 - h)2 = 4(6 - k)
Luego puedes continuar resolviendo, hasta encontrar el vértice de esta paraábola, cuyo parámetro hemos definido.
Y también puedes plantear en forma similar, para el caso de eje de simetría paralelo a OX:
(y - k)2 = 4c(x - h)
y continuar la tarea.
Espero haberte ayudado.