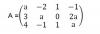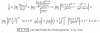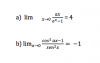-


Antonio Silvio Palmitano
el 18/11/16Consideremos el caso: 1) a = 0.
0 -2 1 -1
3 0 0 0
4 -1 1 0
A la fila 2 la multiplicamos por 1/3:
0 -2 1 -1
1 0 0 0
4 -1 1 0
A la fila 3 le restamos el cuádruple de la fila 2:
0 -2 1 -1
1 0 0 0
0 -1 1 0
A la fila 1 le restamos el doble de la fila 3:
0 0 -1 -1
1 0 0 0
0 -1 1 0
A la fila 3 le sumamos la fila 1:
0 0 -1 -1
1 0 0 0
0 -1 0 -1
Luego, concluimos que en este caso, el rango de la matriz es 3, para a = 0.
Consideremos ahora el caso: 2) a ≠ 0. Tenemos la matriz:
a -2 1 -1
3 a 0 2a
4 -1 1 a
Observa que tenemos tres filas y cuatro columnas, por lo que el rango puede ser a lo sumo igual a 3.
Planteamos el determinante de orden 3 formado por los tres primeros elementos de las filas (están remarcados), desarrollas y queda:
D3 = a2 - 4a + 3, factorizamos y queda:
D3 = (a - 1)(a - 3), luego tenemos tres casos:
1) D3 ≠ 0, que corresponde a: a ≠ 1 y a ≠ 3, y el rango de la matriz es 3.
2) D3 = 0, que nos conduce a dos opciones: 2a) a = 1, y 2b) a = 3 (para los que el rango de la matriz será menor que 3), que estudiamos por separado:
2a) Reemplazamos y la matriz queda:
1 -2 1 -1
3 1 0 2
4 -1 1 1
Observa que la fila 3 es igual a la suma de la fila 1 con la fila 2, luego, tomamos el determinante formado por los dos primeros elementos de las dos primeras filas. lo desarrollas y queda:
D2 = 1 + 6 = 7 ≠ 0, por lo que tenemos que el rango de la matriz es 2.
2b) Reemplazamos y la matriz queda:
3 -2 1 -1
3 3 0 6
4 -1 1 3
A la fila 2 la multiplicamos por 1/3 y queda:
3 -2 1 -1
1 1 0 2
4 -1 1 3
Observa que la fila 3 es la suma de la fila 1 con la fila 2, luego tomamos el determinante formado por los dos primeros elementos de las dos primeras filas, lo desarrollas y queda:
D '2 = 3 + 2 = 5 ≠ 0, por lo que tenemos que el rango de la matriz es 2.
Espero haberte ayudado.
:
-


Antonio Silvio Palmitano
el 18/11/16g) Veamos el numerador y el denominador del primer miembro por separado:
N = sena + cotga = sena + cosa/sena = ( sen2a + cosa)/sena;
D = tana + coseca = sena/cosa + 1/sena = ( sen2a + cosa )/ sena•cosa;
luego planteamos para el primer miembro:
N/D = observa que se simplifican los numeradores = sena•cosa/sena = cosa.
Luego, veamos el segundo miembro:
sena•cotga = sena•cosa/sena = cosa.
h) Veamos el segundo miembro. Distribuimos el denominador y queda:
sen2a/cos2a + sena•cosa/cos2a + cos2a/cos2a =
aplicamos propiedad de un cociente de potencias con exponentes iguales en el primer término, simplificamos en los demás términos y queda:
= (sana/cosa)2 + sena/cosa + 1 =
aplicamos identidad trigonométrica de la tangente en el primer término y queda:
= tan2a + tana + 1 =
ordenamos términos y llegamos a:
= 1 + tana + tan2a.
Espero haberte ayudado.
-
Hola Unicoos. Tengo resuelta la siguiente integral.
Si el ejercicio me pide usar el cambio de variable t = tg(x) y no t = tg(x/2), usando que el sen(x) = 2*sen(x/2)*cos(x/2), ¿cómo relaciono las dos cosas?

David
el 21/11/16(1/senx).(cosx/cosx)= (cosx/senx).(1/cosx) = 1/(tanx. cosx)...
Si haces t=tanx... dt=(1/cos²x).dx... dx=cos²x. dt...
Al sustituir... ∫[1/(t.cosx)].[cos²x. dt] = ∫ dt.cosx / t
Como sec²x= 1/cos²x = 1+tan²x... cos²x= 1/(1+tan²x)... cosx=1/√(1+tan²x)Al sustituir... ∫ dt.[1/√(1+t²)] / t = ∫ dt./(t.√(1+t²)) .. Y ahora intenta acabarla ¿ok?
No tiene sentido que te pidan ese cambio de variable, pero bueno... -
HOLA UNICOOS!
Necesito saber si estos ejercicios están bien hecho por favor. Muchas gracias :D Saludos desde Chile


Antonio Silvio Palmitano
el 18/11/162) Has planteado y resuelto bien el límite del término general an, que tiende a +infinito y, por lo tanto, la serie diverge.
4) Has aplicado el criterio de la raíz y has resuelto bien el límite, por lo que has concluido correctamente que la serie convergen en todo R.
En el otro ejercicio: observa el término general:
an = 6 / 3n = 6•(1/3)n
Luego, la serie queda:
∑(n=0,+inf) ( 6 / 3n ) = ∑(n=0,+inf) ( 6•(1/3)n ) = 6 ∑(n=0,+inf) ( (1/3)n ) = observa que es una serie geométrica con razón 1/3, y observa que -1< 1/3 < 1:
= 6( 1 / (1 - 1/3) ) = 6( 1 / (2/3) ) = 6(3/2) = 9, por lo que concluimos que la serie converge a 9.
En el último ejercicio, has identificado a la "serie p" correctamente, ya que tienes p=5, por lo que resulta ser convergente.
Espero haberte ayudado.
-
Hola Unicoos, tengo un problema al resolver un integral por series de taylor desde 0 a π de ∫sen(x2)dx. Porfavor si podrias ayudarme, que lo llevo intentando y no hay caso. Gracias
P.D: la pagina esta genialisimaa.
-
Hola Unicoos! Necesito ayuda con este ejercicio, lo hice y me da como resultado 11, 54 m/s, pero la respuesta correcta es 20 m/s..
Una moto se desplaza con una rapidez de 10,00 m / s en dirección hacia el Este. Determine que rapidez debe poseer una segunda moto que habiendo partido hacia la dirección Nordeste desde el mismo punto y al mismo tiempo que la primera pero formando un ángulo de 30° con el Norte, siempre se encuentre al Norte de la ruta seguida por la primera moto.
Gracias!


Antonio Silvio Palmitano
el 18/11/16Planteamos las ecuaciones de movimiento. Definimos un sistema cartesiano, con eje OX (O -> E), y eje OY (S -> N), llamamos t al tiempo desde la partida de los móviles, y sabemos que ambos parten desde el origen de coordenadas.
Para el primer móvil (observa que su dirección de movimiento forma un ángulo de 0° con el semieje OX positivo):
x = 10*cos0°*t
y = 0,
resolvemos factores y queda:
x = 10t
y = 0
Para el segundo móvil, llamamos v a su rapidez (observa que su dirección de movimiento forma un ángulo de 60° con el semieje OX positivo):
x = v*cos60°t
y = v*sen60°t, resolvemos factores y queda:
x = (1/2)vt
y = (√(3)/2)vt
Luego, observa que para que el segundo móvil esté constantemente y exactamente al norte del primer móvil, debe cumplirse que las abscisas de sus puntos de posición sean iguales, por lo que planteamos:
(1/2)vt = 10t, luego comparamos expresiones y tenemos:
(1/2)v = 10, multiplicamos por 2 en ambos miembros y llegamos a:
v = 20 m/s
Y con esta rapidez, las ecuaciones de movimiento del segundo móvil quedan:
x = 10t
y = 10√(3)t.
Espero haberte ayudado.
-
Hola unicoos, tengo dudas sobre como resolver esta ecuación trigonometrica. El enunciado dice así: 4senx=sen2x.
Muchas gracias de antemano.


Antonio Silvio Palmitano
el 18/11/16Sustituimos en el segundo miembro de la ecuación, a partir de la identidad: sen2x = 2senxcosx y queda:
4senx = 2senxcosx, dividimos por 2 en ambos miembros y queda:
2senx = senxcosx, hacemos pasaje de término y queda:
2senx - senxcosx = 0, extraemos factor común y queda:
senx(2 - cosx) = 0, luego, por anulación de un producto, tenemos dos opciones:
a) senx = 0, que corresponde a: x = 0, 180°, 360°, 540°, ..., en general: x = 180°•k, con k ∈ Z.
b) 2 - cosx = 0, despejamos y queda: 2 = cosx, que no tiene solución real, ya que el coseno toma valores comprendidos entre -1 y 1.
Por lo tanto, el conjunto solución queda: S = { x ∈ R / x = 180°•k, con k ∈ Z }.
Espero haberte ayudado.
-
Buenas noches. Si fuera tan amable, me gustaría que me ayudase con este ejercicio.
El enunciado dice lo siguiente: Determina un parámetro para obtener un valor dado como resultado de un límite (aplicando L'Hôpital)
Muchas gracias de ante mano por la atención.


Antonio Silvio Palmitano
el 18/11/16a) Observa que el límite es indeterminado, ya que el numerador tiende a cero y el denominador tiende a cero.
Luego, planteamos:
N = ax, y su derivada primera queda: N ' = a,
D = ex - 1, y su derivada primera queda: D ' = ex
Luego, aplicamos la Regla de L'Hôpital:
Lím(x-->0) N/D = Lím(x-->0) N ' / D ' = Lím(x-->0) a/ex = a/1 = a = 4.
b) Observa que el límite es indeterminado, ya que el numerador tiende a cero y el denominador tiende a cero.
Luego planteamos:
N = cos2ax - 1, cuya derivada primera queda:
N ' = -2acosaxsenax = -asen(2ax), luego su derivada segunda queda:
N ' ' = - 2a2cos(2ax).
D = sen2x, luego su derivada primera queda:
D ' = 2senxcosx = sen(2x), y su derivada segunda queda:
D ' ' = 2cos(2x).
Luego, aplicamos la Regla de L'Hôpital:
Lím(x-->0) N/D = Lím(x-->0) N ' / D ' = observa que continúa siendo indeterminado:
= Lím(x-->0) N ' ' / D ' ' = Lím(x-->0) -2a2cos(2ax) / 2cos(2x) = -2a2/2 = - a2= -1,
luego multiplicamos por -1 en la última igualdad, despejamos y tenemos dos opciones.
a1 = -1, a2 = 1.
Espero haberte ayudado.