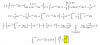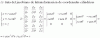-
Laura
el 17/11/16 -
Antoniio
el 17/11/16
Hola, buenas. Estoy trabajando con el método de Lagrange pero no he sabido cómo puedo hacer una transición en esta parte:
Cómo se hace???, gracias de antemano. Saludos !!
David
el 21/11/16Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
Facundo Meier
el 17/11/16Hola profesores, me pueden decir si esta bien esta integral por favor. Muchas gracias
∫ (ln (x)/xdx =∫ u/u du
Sustitución: ln x= u
1/x dx=du
-
Santiago AP
el 17/11/16Hola unicoos, no tengo la menor idea como resolver este ejercicio, si alguien me pudiera ayudar sera excelente, bueno ahi va :
SUPONGA QUE p ES UNA SOLUCION DE Ax=b. SEA Vn CUALQUIER SOLUCION DE LA ECUACION HOMOGENEA Ax=0
y w=p+Vn. muestre que w es una solucion de Ax=b
Antonio Silvio Palmitano
el 17/11/16Tienes que p es solución de la ecuación Ax = b, por lo que puedes plantear:
Ap = b
Tienes que Vn es solución de la ecuación homogénea Ax = O, por lo que puedes plantear:
AVn = 0
Luego, puedes sumar miembro a miembro las ecuaciones remarcadas y queda:
Ap + AVn = b + 0
extraes factor común a izquierda en el primer miembro, resuelves el segundo miembro y queda:
A(p + Vn) = b
Por lo que puedes concluir que w = p + Vn es solución de la ecuación Ax = b.
Espero haberte ayudado.
-
Jordi Ramos
el 17/11/16Hola unicoos necesito su ayuda con esta propiedad, no la puedo resolver por favor ayúdenme
David
el 21/11/16Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
Eduardo Ardaya
el 17/11/16
Muy buenas tardes o noches o buen dia jeje. me plantearon este ejercicio como tarea pero no logro resolverlo porque me pide transformar la ecuacion pero nose que deberia hacer en este caso porque tengo la ecuacion y esta igualada a 0 si despejo x o y llegare a lo mismo se que debo plantearme una funcion Z y otra funcion z pero nose como aplicar la u y v que me dan en el ejercicio ...
alguien de buen corazon que me ayude en este problema se los agradezco
David
el 21/11/16Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
Paul Andia
el 17/11/16
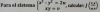buenas tengo estos 2 ejercicios de los cuales estan son mis dudas en el primero donde me pide para el sistema me pide hallar el Jacobi de (x,y/u,v) se como armar el Jacobi pero lo que no puedo es como resolver el ejercicio de antemano agradezco a quien me ayude en esto
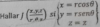y este es el segundo problema el cual es el mismo del anterior pero para este ya no se como aplicar Jacobi para este sistema en este si que no tengo idea de como hacerlo....porfavor alguien ayudeme en estos ejercicios
-
Lucia Romero
el 17/11/16cual sería el mcm de (x-1) ( x+1) (12)
gracias.
Antonio Silvio Palmitano
el 17/11/16Si las expresiones son:
(x-1) que es un binomio elemental,
(x+1) que es un binomio elemental,
12 que es una constante,
el mínimo común múltiplo quedaría: (x+1)(x-1), ya que el máximo común divisor entre los binomios es 1 (o sea son coprimos).
Puedes justificar haciendo las divisiones:
(x+1)(x-1) / (x-1) = (x+1)
(x+1)(x-1) / (x+1) = (x-1)
(x+1)(x-1) / 12 = (1/12)(x+1)(x-1).
Espero haberte ayudado.
-
Velasques Carlos
el 17/11/16
Buenas un favor alguien me puede ayudar con estos 2 ejercicios mis dudas son las siguientes: en el primer ejercicio no se como desarrollar el problema ni como armar mi función porque solo tengo los dados R1 y R2 en Ohm la verdad nose como resolver este ejercicio....
En el segundo Ejercicio me pide transformar la ecuacion a coordenadas polares hasta donde llegue fue armando la funcion V y luego fui derivando porque la Funcion ; V=(x,y) , pero lo que no se es como lo transformo a coordenadas polares....
Antonio Silvio Palmitano
el 17/11/16Para el problema de los resistores en paralelo. Denominemos:
x = R1, y = R2, z = R, luego tenemos: z = xy/(x+y) = xy(x+y)-1.
Luego planteamos las derivadas parciales primeras:
∂z/∂x = y(x+y)-1 - xy(x+y)-2
∂z/∂y = x(x+y)-1 - xy(x+y)-2
Luego, volvemos a derivar a cada una con respecto a la misma variable:
∂2z/∂x2 = - 2y(x+y)-2 +2xy(x+y)-3 = (x+y)-3 (- 2y(x+y) + 2xy) = - 2y2(x+y)-3
∂2z/∂y2 = - 2x(x+y)-2 + 2xy(x+y)-3 = (x+y)-3 (- 2x(x+y) + 2xy) = - 2x2(x+y)-3Luego planteamos el producto entre las derivadas parciales segundas:
∂2z/∂x2 • ∂2z/∂y2 = 4x2y2 • (x+y)-6 = 4 x2y2 (x+y)-2 • (x+y)2 (x+y)-6 = 4 ( xy(x+y)-1 )2 ) • (x+y)-4 = 4z2 / (x+y)4.Espero haberte ayudado.
-
Dipika Holos
el 17/11/16
