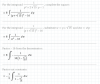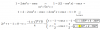Paso a paso:

Está bien planteado, Magalí.

Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas

Son matrices elementales todas aquellas que se obtienen a partir de la matriz identidad, aplicando operaciones elementales.

a) A partir de la matriz I₃ a la fila 2 se le sumó el doble de la fila 1, y luego a la fila 3 se le sumó el triple de la fila 1. 

b) A partir de la matriz I₃ a la fila 1 se le sumó el triple de la fila 2, luego a la fila 1 se le sumó el cuádruple de la fila 3, y luego a la fila 2 se le sumó el doble de la fila 3.

c) A partir de la matriz I₄ a la fila 2 se le sumó la fila 1, y luego a la fila 4 se le sumó la fila 3.

d) A partir de la matriz I₄ a la fila 1 se le restó la fila 2.

Por lo que tenemos, todas son matrices elementales.

Espero haberte ayudado.

Aaahh... yo tenía entendido que únicamente se podía aplicar UNA operación elemental, de forma que si sumaba una fila con otra ya no podía volver a hacerlo. Pero nada, todo aclarado ;) ¡¡¡Muchas gracias por tu respuesta!!! :))

PD: si alguien pudiese aclararme lo de la imagen estaría muy agradecida :)

Aunque ahora que lo compruebo en internet, según Wikipedia:

Una matriz elemental de orden n es el conjunto de matrices que se obtienen de la matriz identidad ${\displaystyle I_{n}}$ aplicando solo una operación elemental de fila o columna:

• Por escalamiento (intercambio de filas)
• Producto de fila por un escalar o suma de una fila con una combinación lineal de otras (eliminación)
• Por permutación

El símbolo extraño que aparece quiere decir I_{n  ,} en Wikipedia estaba escrito en LaTeX y el foro no lo reconoce.

Observa que si divides la segunda ecuación con la primera, obtienes:

dy/dx = (5x + 3y) / (x + 3y)

Luego proponemos: y = xw, de donde tenemos: dy/dx = w + xdw/dx, luego sustituimos y queda:

 w + xdw/dx = (5x + 3xw) / (x + 3xw), extraemos factor común y simplificamos en el segundo miembro y queda:

 w + xdw/dx = (5 + 3w) / (1 + 3w), hacemos pasaje de término y queda:

xdw/dx = (5 + 3w) / (1 + 3w) - w, extraemos denominador común en el segundo miembro y queda:

xdw/dx = (5 + 3w - w - 3w²) / (1 + 3w), resolvemos el numerador del segundo miembro y queda:

xdw/dx = (5 + 2w - 3w²) / (1 + 3w), luego hacemos pasajes de divisores y factores para separar variables y queda:

(1 + 3w)dw/(5 + 2w - 3w²) = dx/x, luego puedes integrar miembro a miembro (observa que a la izquierda debes aplicar fracciones parciales, y a la derecha es directa).

Queda para que continúes la tarea.

Espero haberte ayudado.

De otra manera

Va una orientación; sustituye sen²x = 1 - cos²x y queda:

1 = 2(1 - cos²x) - cosx, luego sustituyes: t = cosx y queda:

1 = 2(1 - t²) - t, distribuyes, haces pasajes de términos, ordenas y queda:

2t² + t - 1 = 0.

Luego, queda para que continúes la tarea (observa que t debe tomar valores comprendidos entre -1 y 1).

Espero haberte ayudado.

vale muchas gracias

pero una cosa, la t que es? tangente?

Mi pregunta sigue siendo, que es t?

No, es una letra cualquiera, para que se vea la ecuación de 2º grado.

Muchas gracias!! :)

Por cierto me podrías ayudar con otra ecuación?

4·sinx + 2·cos(2·x)=3

Interés Simple y Compuesto

¿Está bien copiada?

Disculpa el ejercicio dice asi 

Dar solucion al sistema de ecuaciones diferenciales:

 dx/dt=x+3y

dy/dt= 5x+3y 

Espero puedas ayudarme

Para una matriz cuadrada de orden 2, el polinomio característico tiene como término independiente el determinante. Entonces, si det(A)=1, distinto de 0, la matriz tiene inversa.

Imagino que está bien, por lo menos el procedimiento, los que son lienaealmente dependiente y sº generador ( que son ) es base, y a partir de ahí atribiyéndole un parámetro, te salen las paramétricas, aunque primero, ese polinomio se pasa a base, y después de base a paramétricas, y un consejillo, yo pondría letras diferentes de lambda tal que alfa lambda beta gamma o mu, ya que después en cartesianas te puedes liar un poco, espero haberte ayudado

Está bien, Miquel.

Te mando una resolución alternativa.