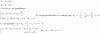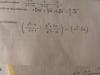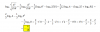-
Jordi Ramos
el 10/11/16Hola amigos tengo una duda en el apartado c de este ejercicios no entiendo que me pide....le agradecería su ayuda
-
Juan Carlos Bonet
el 10/11/16 -
Javier García
el 10/11/16 -
Raisa
el 10/11/16En estas ecuaciones:
Necesito ayuda Antonio con estas ecuaciones:
Hola necesito ayuda con estas ecuaciones :
6º Resuelve la ecuación: sen(3x) – sen 30º = 0
(1punto)
Hice esto yo sola:
Se que hay que poner el seno 3x en función de seno 30 sabiendo cuanto vale seno30º( A partir de ahí no se seguir)
7º Resuelve la ecuación: senx= 1+ 2 cos( Se que tengo que poner 2 cos en función de seno ( A partir de ahí no se como seguir)
(1punto)
Un saludo
Antonio Silvio Palmitano
el 10/11/166°) Tienes la ecuación trigonométrica:
sen(3x) – sen 30º = 0, haces pasaje de término y queda:
sen(3x) = sen30°, reemplazamos en el segundo miembro, tal como dices:
sen(3x) = 1/2, luego componemos con la función inversa del seno,
y observa que tenemos dos opciones (una en el primer cuadrante, y otra en el segundo cuadrante):
a) 3x = 30° + 360° * k, con k ∈ Z, dividimos en todos los términos de la ecuación por 3 y queda:
x = 10° + 120° * k, con k ∈ Z.
b) 3x = 150° + 360° * m, con m ∈ Z, dividimos en todos los términos de la ecuación por 3 y queda:
x = 50° + 120° * m, con m ∈ Z.
7°) Si la ecuación es:
senx = 1+ 2cosx, observa que el coseno debe tomar valores negativos para que la ecuación tenga sentido,
luego elevas al cuadrado en ambos miembros y queda:
(senx)^2 = (1 + 2cosx)^2, desarrollas en el segundo miembro y queda:
(senx)^2 = 1 + 4cosx + 4(cosx)^2, sustituyes en el primer miembro por la expresión equivalente y queda:
1 - (cosx)^2 = 1 + 4cosx + 4(cosx)^2, haces pasaje de términos, reduces términos semejantes y queda:
-5(cosx)^2 - 4cosx = 0, multiplicas en todos los términos de la ecuación por -1, extraes factor común y queda:
cosx(5cosx - 4) = 0, luego, por anulación de un producto, tenemos dos opciones:
a) cosx = 0, que al reemplazar en la ecuación inicial nos queda: senx = 1, y tenemos x = 90° + 360° * k, con k ∈ ℤ.
b) 5cosx - 4 = 0, que nos conduce a: cosx = 4/5, que al sustituir en la ecuación inicial nos queda:
senx = 1 + 2*4/5 = 13/5 > 1, lo que resulta absurdo, como indicamos anteriormente.
Espero haberte ayudado.
Espero haberte ayudado.
-
Raisa
el 10/11/16Antonio en este ejercicio :
5º Calcula los ángulos de un triángulo cuyos lados miden a=2cm; b=4cm; c=5cm
Hice esto yo sola :Se que el semiperímetro del triángulo es p = (a+b+c)/2., por lo tanto seria :tan(α/2) = V( (p-b)(p-c) / p(p-a) )
tan(β/2) = V( (p-a)(p-c) / p(p-b) )
tan(γ/2) = V( (p-a)(p-b) / p(p-c) )
Y a partir de aqui no se como continuar.
Un saludo
Antonio Silvio Palmitano
el 10/11/16Hacemos los cálculos:
p =(2+4+5)/2 = 11/2 = 5,5
p-a = 5,5-2 = 3,5
p-b = 5,5 - 4 = 1,5
p-c = 5,5 - 5 = 0,5.
Luego, vamos con el primer cálculo (los demás son parecidos).
tan(α/2) = V( (p-b)(p-c) / p(p-a) ) = V( 1,5*0,5 / 5,5*3,5 ) = V( 0,75/19,25 ) ≅ V(0,039) = 0,197,
luego componemos con la función inversa de la tangente y queda:
α/2 ≅ 11,17°, multiplicas por 2 en ambos miembros y llegas a: α ≅ 22,34°.
Espero haberte ayudado.
-
Andrea
el 10/11/16Hola, necesito ayuda con este ejercicio:
Utiliza el teorema de Bolzano para probar que la ecuación 2x3+3x2-0.2=0 tiene raices en los intervalos (-2,-1), (-1,0), (0,1).
Antonio Silvio Palmitano
el 10/11/16Primero observa que la función cuya expresión es: f(x) = 2x3+3x2-0.2 es continua en toda la recta real, y en particular en los intervalos.
Luego, vamos con el primer intervalo (para los demás, la tarea es similar):
Primero, evaluamos en los extremos del intervalo cerrado correspondiente [-2 , -1]:
f(-2) = -16 + 12 - 0,2 = -4,2 < 0
f(-1) = -2 + 3 - 0,2 = 0,8 > 0
Luego, por el Teorema de Bozano, como la función toma valores con signos distintos en los extremos del intervalo [-2 , -1 ],
existe c perteneciente al intervalo (-2,-1) tal que f(c) = 0.
Espero haberte ayudado.
-
Raisa
el 10/11/16
Antonio Benito tengo una duda
Enunciado:
Desde dos puntos A y B situados en la misma orilla de un río y distantes entre sí 80 m, se observa un punto C situado en la orilla opuesta, bajo ángulos de 60º y 45º, respectivamente. Calcula las distancias desde los puntos A y B al punto C.α = 60°, β = 45°, γ = 75°, para los ángulos con vértices A, B y C, respectivamente.
Esto fue lo que hize:
Observo que el lado opuesto al vértice C, le denomino c y que tiene 80m de longitud, nos preguntan las longitudes de los otros dos lados: b (opuesto al vértice B) y a (opuesto al vértice A).
A partir del Teorema del Seno
a) senα / a = senγ / c, de donde puedes despejar a = c*senα / senγ
Puse estos datos están bien? pero a partir del teorema no se habría hacerlo puedes echarme una mano?
Antonio Silvio Palmitano
el 11/11/16Si, está bien, y la ecuación anterior a la remarcada corresponde al Teorema del Seno. Luego reemplazas y queda:
a = 80*sen60°/sen75°, y solo te queda hacer el cálculo.
El Teorema del Seno es aplicable a todo triángulo con ángulos interiores α , β, γ, cuyos lados opuestos tienen longitudes a, b, c, respectivamente, y se cumple:
senα / a = senβ / b = senγ / c,
y observa que hemos empleado la igualdad del primer miembro con el tercero para poder calcular la longitud a.
Espero haberte ayudado.
-
Miquel Martos Doroteo
el 10/11/16El segundo método lo adjunto aquí.
Antonius Benedictus
el 10/11/16Ambos métodos son correctos. La base de un subespacio vectorial no es única, por lo que la solución puede adoptar formas distintas.
Mi consejo: una vez que determinas el rango "r" de la matriz de coordenadas (que va a ser la dimensión del subespacio), en dicha matriz (sin manipular por Gauss) busca un menor distinto de cero de otden "r" (menor básico). Puedes estar seguro que los vectores que forman parte de dicho menor son l.i. y constituyen una base del subespacio.
-
Miquel Martos Doroteo
el 10/11/16Muy buenas tardes a todos, me gustaría que me aclarasen unas dudas respecto el tema de Álgebra Lineal. Estoy realizando un ejercicio donde me piden encontrar una base del sub-espacio dado, y lo estoy realizando de dos formas, la primera es como lo explican los profesores de mi universidad y la segunda como lo vi en un vídeo de youtube. Les adjunto las dos, ¿cuál es mejor?
También he observado que los dos métodos me dan diferentes bases, ¿a que es debido esto?
Muchas gracias por la ayuda.
chado
el 10/11/16como decir mejor no se, (igual solo veo una), con respecto a la base pudes obtener distinta, pero lo mas seguro es que sea una multiplo de la otra, y de los otros metodos, dependeria, se que hay unos metodos que son mas largos y lo resolverias con matrizes en 3 pasos, pero expresandolos como combinacion lineal te puede servir para matrices de cambio de cordenadas y eso.
-
carmen ruiz
el 10/11/16Buenas,necesito ayuda en el.tema de las funciones y derivadas,y es que no se como buscar la.relacion entre la gráfica de la.funcion y la de su derivada. Además,me gustaría también haceros una pregunta,¿como puedo saber el grado de.una.funcion a partir de su gráfica?
Adjunto foto por si no me.he explicado bien
