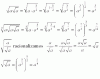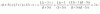-
Ayuda con estos ejercicios:
61-Valorar el error que se comete cuando se aproxima el número e por la cantidad 2 +(1/2!)+(1/3!)+(1/4)!
62-Hallar la aproximación cuadrática de la función f(x) = sen2x en x = 0 y determinar el correspondiente resto. Acotar superiormente este resto para |x| < 0.5. ¿son correctos?


Antonio Silvio Palmitano
el 11/11/1661. Se ha aproximado el valor de e^1 por medio de un Polinomio de Taylor de orden 4, con centro de desarrollo xo = 0, de la función f(x) = e^x, con x = 1.
Luego, por medio de la fórmula del Resto de Lagrange, tenemos:
R(x) = ( e^c / 5! )x^5, que evaluado para x = 1 queda:
R(1) = ( e^c / 120 ), con 0 ≤ c ≤ 1.
Luego, pasamos a acotar (observa que e^0 ≤ e^c ≤ e^1 ≤ 3):
| R(1) | = ( e^c / 120 ) = ( e^c / 120 ) ≤ ( e^1 / 120 ) ≤ 3/120 = 1/40.
Por lo tanto, el error cometido es menor o igual que 1/40.
62. Planteamos:
f(x) = sen²x, y f(0) = 0
f ' (x) = 2*senx*cosx, y f ' (0) = 0
f ' ' (x) = 2cos²x - 2sen²x, y f ' ' (0) = 2
f ' ' ' (x) = -8senx*cosx, y f ' ' '(c) = -8senc*cosc, con 0 ≤ c ≤ 0,5.
Luego, el Polinomio de Taylor de orden 2, con centro de desarrollo xo = 0 queda:
P(x) = (2/2!)x² = x².
Luego, por medio de la fórmula del Resto de Lagrange, tenemos:
R(x) = ( -8senc*cosc / 3! )x^3, con 0 ≤ c ≤ 0,5. Luego, evaluamos para x = 0,5 y queda:
R(0,5) = ( -8senc*cosc / 6 )*0,5^3 = -senc*cosc / 6.
Luego pasamos a acotar (observa que |senc| ≤ 1 y |cosc| ≤ 1):
R(0,5) ≤ | R(0,5) | = | -senc*cosc / 6 | = |senc|*|cosc| / 6 ≤ 1*1/6 = 1/6.
Por lo que concluimos que el error cometido es menor o igual que 1/6.
Espero haberte ayudado.
-
-
Necesito ayuda con este ejercicio de bachillerato por favor, soy incapaz de hacerlo y llevo mucho intentándolo... Creo que al dar click en la imagen funciona, de todas formas dejo el link aquí también

https://i.gyazo.com/6505454d218574d862c3d1176abb66b5.png
-


Antonio Silvio Palmitano
el 10/11/16Observa que la fila 2 sumada con el doble de la fila 3 es igual a la fila 4, por lo que la fila 4 es combinación lineal de las filas 2 y 3, y puedes descartarla para calcular el rango de la matriz.
Luego, como tienes que el rango de la matriz es tres, puedes considerar los tres primeros elementos de las tres primeras filas, plantear con ellos un determinante de orden tres, desarrollarlo, y analizar a partir de la ecuación que te queda que sea distinto de cero.
Haces el desarrollo según la primera fila, o con la Regla de Sarrus, y queda:
D = x(9-10) -y(0+5) + z(0-3) = -x - 5y - 3z, luego planteamos:
D ≠ 0, sustituimos y queda:
-x - 5y - 3z ≠ 0, de donde puedes despejar:
-5y - 3z ≠ x.
Con esta condición, ya tenemos que el determinante de orden tres es distinto de cero y, por lo tanto la matriz es de rango tres.
Y si tenemos que x = -5y - 3z, podemos plantear un nuevo determinante de orden tres, con los tres últimos elementos de las tres primeras filas, desarrollarlo, y plantear que debe ser distinto de cero, tal como hecho en el desarrollo anterior. Queda la tarea para que la concluyas.
Espero haberte ayudado.
-
Hola me podéis corregir este ejercicio:
Se depositan 10 000 € a un interés compuesto del 4% anual durante tres años. Calcula el capital final si el periodo de capitalización es mensual.
-
Necesito encontrar un numero complejo Z= a+bi que cumpla la siguiente ecuación:
(1+5i)*Z+(3+i) = 12i
-
Hola podrias ayudarme con este ejercicio- por la regla de la cadena: 1/ [ (sen ²) (2x +1)]


Antonio Silvio Palmitano
el 10/11/16Puedes comenzar por escribir la expresión de la función como una expresión con exponente negativo:
y = ( sen(2x+1) )^(-2), luego derivas (observa que tienes una potencia, cuyo argumento es un seno, cuyo argumento es un binomio):
y ' = -2( sen(2x+1) )^(-3) * cos(2x+1) * 2 = -4cos(2x+1) / ( sen³(2x+1) ).
Espero haberte ayudado.










 Hola, lo primero de todo muchas gracias y lo segundo es si podría decirme si mi razonamiento estaría bien, esto es a lo que he conseguido llegar pero no estoy muy seguro...
Hola, lo primero de todo muchas gracias y lo segundo es si podría decirme si mi razonamiento estaría bien, esto es a lo que he conseguido llegar pero no estoy muy seguro...