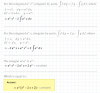-
Hola a todos!! necesito ayuda con este ejercicio:
Hallar el numero de vectores linealmente independientes que hay en el conjunto
S = (1; 1; 1); (0; 2; 1); (2; 0; -3); (-1; 1; 2)
Muchas gracias por adelantado!!!!
-
Buenos días, tengo problemas para resolver el ejercicio 7 y 8. El gráfico que se ubica en la esquina inferior derecha del punto 8 no va, ese gráfico corresponde a otro ejercicio. Si pudieran hacer un vídeo para resolver la duda seria de mucha ayuda. Muchas gracias.


chado
el 10/11/16para comprobar la continuidad, f(x0) tiene que existir y ademas lim x+-->x f(x) = lim x--->x f(x) y ademas tiene que ser igual a f(x)
para este casi
f(1) tiene que existir y los limites laterales tienen que ser iguales entre si e igual a f(x)
primero f(1)=1
ahora veo los limites laterales
por derecha
lim x2=1
x-->1+
por izquierda
lim -2x+3= 1
x-->1-
ahora como los limites laterales coinciden y es igual a la funcion evaluada en dicho punto, podes asegurar la continuidad
-
Hola, pido ayuda a los profesores Antonio y César, tengo este ejercicio y me piden demostrar las 7 propiedades que se tienen que cumplir para que este sea un espacio vectorial. Gracias
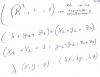


chado
el 10/11/16tecnicamente con demostrar 3 ya demostrarias los demas axiomas
que el sub espacio sea distinto del nulo, osea que tenga algun elemento.
que la suma de dos elementos cualquiera del subespacio pertenecen al subespacio ("v" y "w" pertenecientes al subespacio (v+w) tambien pertenece al subespacio)
y que "k" real y v un vector de de tu subespacio ( k.v tambien pertenece al subespacio)
pero como bien dijo el maestro Antonio, es solo paciencia y aplicacion, mas no se puede reducir el trabajo.
-
Antonio me puedes ayudar? gracias
º Desde dos puntos A y B situados en la misma orilla de un río y distantes entre sí 80 m, se observa un punto C situado en la orilla opuesta, bajo ángulos de 60º y 45º, respectivamente. Calcula las distancias desde los puntos A y B al punto C.
(1,5 puntos)
5º Calcula los ángulos de un triángulo cuyos lados miden a=2cm; b=4cm; c=5cm

Gabriel
el 10/11/16Echa un vistazo a Trigonometria - Resolucion de un triangulo
y también a Trigonometria -Teorema del coseno
-
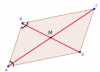
A partir del paralelogramo ABCD donde:
A= (-2,-2)
B=(1,1)
C=(6,2)
D= (3,-1)
Decidme si estas respuestas son correctas:
El perímetro es 18,69.
Las coordenadas del punto M son (2,0)
¿Como puedo calcular el angulo interno del vértice de A i B?


David
el 10/11/16Halla el vector AD y el vector Ab. Aplica producto escalar y sabrás el angulo que forman...
Por otro lado, tampoco es complejo hallar el perimetro si obtienes los vectores de cada lado y hallas su modulo..
No necesitas obtener el angulo que forman para ello..
PRODUCTO ESCALAR y VECTORIAL de dos vectores

Antonio Silvio Palmitano
el 11/11/16Comencemos por plantear las componentes de los vectores:
AB = <3,3> = DC, y también AD = <5,1> = BC.
Luego planteamos sus módulos:
|AB| = |DC| = √(18) = 3√(2), y también |AD| = |BC| = √(26).
Luego, planteamos el perímetro del paralelogramo:
p = |AB| + |DC| + |AD| + |BC| = 2*3√(2) + 2√(26) = 6√(2) + 2√(26) ≅ 18,68.
Luego pasamos al cálculo de la medida del ángulo interior con vértice A, y procedemos como indica el colega David:
AB•AD = <3,3>*<5,1> = 3*5 + 3*1 = 18
AB•AD = |AB|*|AD|*cosα = 3√(2)*√(26)*cosα = 3√(52)*cosα = 3*2√(13)*cosα = 6√(13)*cosα.
Luego igualamos y queda la ecuación:
6√(13)*cosα = 18, de la que despejamos:
cosα = 3/√(13), luego componemos con la función inversa del coseno y llegamos a:
α ≅ 33,69°.
Luego, como el ángulo interior con vértice B es suplementario con α, tenemos:
β = 180° - α ≅ 146,31°.
Luego, observa que M es el punto medio de la diagonal con extremos en los puntos A y C, por lo tanto planteamos para las coordenadas del punto M:
M( (-2+6)/2 , (-2+2)/2 ), por lo que tenemos que las coordenadas del punto son: M(2,0).
Por lo que se puede apreciar, tus respuestas son correctas.Espero haberte ayudado.
-
Antonio teniendo estos datos como hago la ecuación ?
α = 60°, β = 45°, γ = 75°, para los ángulos con vértices A, B y C, respectivamente.
Luego, observa que el lado opuesto al vértice C, lo denominamos c, tiene 80m de longitud, y que nos preguntan las longitudes de los otros dos lados: b (opuesto al vértice B) y a (opuesto al vértice A).
A partir del Teorema del Seno
a) senα / a = senγ / c, de donde puedes despejar a = c*senα / senγ
5- Puedes aplicar el Teorema de las tangentes, y llamamos al semiperímetro del triángulo: p = (a+b+c)/2.
tan(α/2) = V( (p-b)(p-c) / p(p-a) )
tan(β/2) = V( (p-a)(p-c) / p(p-b) )
tan(γ/2) = V( (p-a)(p-b) / p(p-c) )
Como hallo los cálculos? Ayudame porfavor tengo el viernes el examen
-
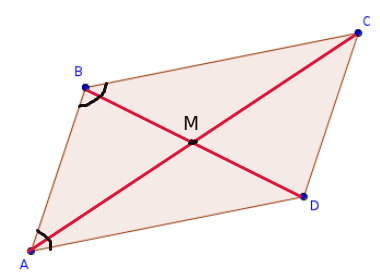
A partir del paralelogramo ABCD donde:
A= (-2,-2)
B=(1,1)
D= (3,-1)
¿Como encuentro las coordenadas del punto C? (Utilizando la igualdad de vectores que representa lados opuestos)

Gabriel
el 10/11/16Hola Juan.
Sí, para hallar el perímetro, hay que sumar las distancias de los vectores, Perímetro = AB + BC + CD + DA.
Otra cosa es que al ser un paralelogramo, tienes que AB=CD, y BC=DA, por lo que puedes reducir la ecuación a: Perímetro = 2 AB + 2 BC
¿Así mejor?
Y no, no he encontrado ningún video de unicoos referente a paralelogramos y en relación a vectores.
Saludos.

Gabriel
el 11/11/16Juan, está bien resuelto, perfecto...!!! Mi enhorabuena.
Es más, cuando lo he calculado para comprobar, me he dado cuenta que también puedes resolverlo de la siguente forma. Perímetro = 2 AB + 2 AD
Así, podrías calcular el perímetro sin la necesidad de calcular C.
O dicho de otra forma. Aunque calcules C, no tienes porqué utilizarlo para calcular el perímetro.
Saludos.
-
∈Buenos días.
Si algún unicoos puede ayudarme con esta desigualdad de valor absoluto:
Ι 2x - 7/3 Ι > 13/2 ; si continúo, digo: 2x - 7/3 < - 13/2 ∪ 2x - 7/3 > 13/2 no se continuar y no encuentro info que continúe.
Otra es esta que logro un resultado del revés al que me dan con el ejercicio:
Ι 8 -3x Ι > 32 ; 8 -3x < 32 ∪ 8 -3x > 32 ; -3x < -32 -8 ∪ -3x > 32 -8 ; -3x/3 < -40/3 ∪ -3x/3 > 24/3 ; x ¿>? ∪ x ¿>? x∈ ( -40/3, - ∞) y x∈ (8, + ∞)
Donde el resultado que me dicen que es correcto es:
x∈(-∞, -8) y x∈(40/3,∞) este revés no lo controlo.Y esta, la que si logré hacer:
Ι 4x/5 +2 Ι < 12 ; -12 < 4x/5 + 2 < 12 ; -12*5 < 4x/5 +2*5< 12*5 ; -60 < 4x+ 10 < 60 ; -60 -10 < 4x +10 -10 < 60 ; -70 < 4x < 50 ; -70/4<4x/4<50/4 ; -70/4<x<5'/4
x∈ (-70/4,50/4)
Gracias.


Antonio Silvio Palmitano
el 10/11/16Debes recordar cómo son los desarrollos de las desigualdades con valor absoluto (a es un número real positivo):
1) |u| < a ↔ -a < u < a; o también: |u| ≤ a ↔ -a ≤ u ≤ a.
2) |u| > a ↔ u < -a ∨ u > a; o también: |u| ≥ a ↔ u ≤ -a ∨ u ≥ a.
a) | 2x -7/3 | > 13/2, luego por el desarrollo (2):
2x - 7/3 < -13/2 ∨ 2x - 7/3 > 13/2, hacemos pasaje de término en ambas inecuaciones, resolvemos y quedan:
2x < -25/6 ∨ 2x > 53/6, dividimos por dos en ambos miembros en las dos inecuaciones, resolvemos y quedan:
x < -25/12 ∨ x > 53/12, luego expresamos como intervalos:
x ∈ (-∞ , -25/12) ∪ (53/12,+∞).
b) | 8 - 3x | > 32, luego por el desarrollo (2):
8 -3x < -32 ∨ 8 - 3x > 32, hacemos pasaje de término en ambas inecuaciones, resolvemos y quedan:
-3x < -40 ∨ -3x > 24, multiplicamos por -1/3 en ambas inecuaciones (observa que cambian los sentidos de las desigualdades), resolvemos y quedan:
x > 40/3 ∨ x < -8, luego expresamos como intervalos:
x ∈ (-∞,-8) ∪ (40/3,+∞).
c) Ι 4x/5 +2 Ι < 12, por el desarrollo (1):
-12 < 4x/5 + 2 < 12, multiplicamos por 5 en todos los términos de la doble inecuación (observa que no cambian los sentidos de las desigualdades):
-60 < 4x + 10 < 60, restamos 10 en todos los miembros de la doble inecuación, resolvemos y queda:
-70 < 4x < 50, dividimos por 4 en todos los miembros de la doble inecuación, resolvemos y queda:
-35/2 < x < 25/2, luego expresamos como intervalo y queda:
x ∈ (-35/2 , 25/2).
Espero haberte ayudado.


Manu
el 24/11/16Repasando ahora es que no entiendo por que se tiene que multiplicar por - 1/3 en
| 8 - 3x | > 32 8 -3x < -32 U 8 - 3x > 32 ; -3x < -40 U -3x > 24 ; -1/3 (-3x) < -40 U -1/3 (-3x) > 24 ; x > 40/3 U x < -8 x ∈ (-∞,-8) ∪ (40/3,+∞).
Veo que -1/3 multiplica pero no entiendo por que. Es por ser un número negativo -3x o, por que es -1/3 y no otra fracción?
gracias


Manu
el 24/11/16Y para el último en c) Ι 4x/5 +2 Ι < 12 -12 < 4x/5 + 2 < 12 multiplico por 5 todo pero, así? 5 · (-12) < 4x + (5 · 12) < 5 · 12 para luego quedar
-60 < 4x + 10 < 60 -60 -10 < 4x ++10 -10 < 60 -10 -70 < 4x < 50 - 70/4 < 4x/4 < 50/4 -32/2 < x < 25/2 x∈ (-35/2 , 25/2)
Por que en los primeros apuntes multiplique 5 · (-12) < 5 · (4x +12) < 5 ·12