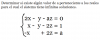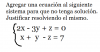-


David
el 7/11/16Para el primero.. Teorema de Rouche
Para el segundo basta con añadir una ecuacion con los mismos terminos en x,y,z pero distinto termino independiente... Por ejemplo x+y-z=0Se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)
-
Hola unicoos como puedo subir pdf

Ángel
el 6/11/16Haz una/s captura/s de pantalla con el/los ejercicio/s:
- Abre el PDF
- Para realizar una captura de la pantalla completa, pulse el botón Imprimir pantalla (también puede estar etiquetado como Impr pant o PrtScrn) del teclado. Puede estar cerca de la parte superior, a la derecha de todas las teclas F (F1, F2, etc.) y a menudo en línea con las teclas de flecha.
- Para realizar una instantánea sólo del programa que está activo, mantenga pulsado el botón Alt(situado en cualquiera de los lados de la barra espaciadora) y, a continuación, pulse el botón Imprimir pantalla.
- Para ver esta instantánea o guardarla como una imagen, puede utilizar Microsoft Paint (Paint) o cualquier otro programa de gráficos. Le recomendamos que utilice el programa Paint.
- Para abrir el programa Paint en el sistema, vaya a Inicio -> Programas -> Accesorios->Paint
- En la página en blanco de Paint, haga clic en Editar y, a continuación, haga clic en Pegar y la captura de pantalla aparecerá en la página en blanco.
- Para guardar, realice los pasos habituales para guardar una imagen o gráfico (por ejemplo, haga clic en Archivo, Guardar como o Guardar.)
- Seleccione la ubicación que desee (unidad/carpeta) para guardar el archivo. La ubicación por defecto es el Escritorio. Escriba el nombre que desee en Nombre de archivo. También puede seleccionar el tipo de imagen que desee haciendo clic en la opción Guardar como tipo en el menú desplegable. Por ejemplo, aquí estamos guardando el archivo 'screenshot01' como tipo .PNG (recomendado).
- Y por último, adjuntas la imagen AQUÍ en tu comentario pulsando en el icono de "imagen" (el tercero empezando por la derecha), seleccionas el archivo y lo envias
(lo de subir un pdf aquí es innecesario e ineficiente, creo)
-
Hola unicoos, necesito ayuda para resolver este ejercicio:
Calcula el tiempo que tiene que permanecer un capital de 3000 euros con un interés compuesto del 6% cuando su capitalización es semestral para dar lugar a un capital final de 5000 euros? Se tiene que hacer mediante logaritmos. Muchas gracias ;)
-
Hola unicoos necesitaría de su ayuda con este problema, dice así:
operar y expresar como una única fracción y sin paréntesis.
1) 1/a+h - 1/h todo esto dividido h
2) (1+x∧-1) ² - (1-x∧-1)²
eso es todo gracias, espero que se entienda. "al ∧ lo eh puesto como elevado"
-
Buenas, ¿infinito/0 seria una indeterminación? Al calcular la sustitucion ingenua de un limite me queda eso y no se si seria una indeterminacion..
-


Antonio Silvio Palmitano
el 6/11/16Observa que el numerador puede escribirse (indicamos raíz cúbica con (3V)): N = 7 - (3V)(2²), y que el denominador puede escribirse: D = (3V)(2² * 3).
Luego, como el denominador consta de un solo término (es unimembre), multiplicamos al numerador y al denominador por: (3V)(2 * 3²) y la expresión queda:
Numerador = ( 7 - (3V)(2²) ) * (3V)(2 * 3²) = distribuimos:
= 7 * (3V)(2 * 3²) - (3V)(2²) * (3V)(2 * 3²) = asociamos raíces en el segundo término:
= 7 * (3V)(2 * 3²) - (3V)(2³ * 3³) = simplificamos raíz y potencias en el segundo término:
= 7 * (3V)(2 * 3²) - 2*3 = - 6 + 7 * (3V)(2 * 3²).
Denominador = (3V)(2² * 3) * (3V)(2 * 3²) = asociamos raíces:
= (3V)(2³ * 3³) = simplificamos raíz y poencias:
= 2*3 = 6.
Luego, la expresión queda:
Numerador / Denominador = ( - 6 + 7 * (3V)(2 * 3²) / 6 = -1 + (7/6) * (3V)(2 * 3²) = -1 + (7/6) * (3V)(18).
Espero haberte ayudado.
-
Me podeis decir si tengo bien los deberes
Enunciado
aplica la divisibilidad
51:si la diferremcia entre la suma de las cifras de lugar por y las suma de las cifras de lugar impar es 0 o divisible por 11
512:si la ultima cifra es 0 o par
5125:si la ultima cifra es 0 o 5
51.250:Si la ultima cifra es 0
otro: di todos los criterios menos el del 11
2: si la ultima cifra es 0 o par
3:si la sumas de sus cifras es divisible por 3
5:si la ultima cifra es 0 o 5
10:si la ultima cifra es 0


David
el 7/11/16Del primero no sabría que decirte porque no adjuntas el enunciado exacto y no tengo ni idea de que te piden.
En cuanto a los criterios, correcto.. Por cierto.. ¿has visto este video?... Criterios de divisibilidad 01 -


Antonio Silvio Palmitano
el 6/11/16Tienes el sistema de tres ecuaciones con dos incógnitas
x + ay = 1
-x + ay = -1, hacemos pasaje de términos y queda: ay + 1 = x (*)
x + y = a
Sustituimos la expresión (*) en la primera y en la tercera ecuación, y el sistema queda:
ay + 1 + ay = 1,
ay + 1 + y = a
Reducimos términos semejante y cancelamos términos en la primera ecuación, y queda: 2ay = 0,
dividimos por 2 en ambos miembros y queda: ay = 0, que nos conduce a dos opciones:
a) y = 0, que al sustituir, la segunda en la segunda ecuación queda: a = 1, y al reemplazar en la ecuación señalada (*) nos queda: 1 = x.
b) a = 0, que al sustituir en la segunda ecuación queda: y = -1, y al reemplazar en la ecuación señalada (*) nos queda: 1 = x.
Luego, tenemos dos opciones para este problema:
a) si a = 1, la solución es x = 1 e y = 0,
b) si a = 0, la solución es x = 1 e y = -1.
Espero haberte ayudado.
-
Hola unicoos como están, quisiera que me ayuden con estos dos problemas se los agradecería, aquí están:
a)el número entero que antecede a -5/3 es :
b)el número entero consecutivo de -3/5 es:
eso es todo por ahora gracias.

Ángel
el 6/11/16Números enteros: compuesto por todos los números naturales positivos y negativos y el cero (........,-4,-3,-2,-1,0,1,2,3,4,....)
a)¿Entre qué números enteros está -5/3? Entre -2=-6/3 y -1=-3/3
¿Qué número es su antecesor (va antes)? EL -2 ES EL NÚMERO ENTERO QUE ANTECEDE A -5/3
b)¿Entre qué números enteros está -3/5? Entre -1=-5/5 y 0=0/5
¿Qué número es es consecutivo (va después)? EL 0 ES EL NÚMERO ENTERO QUE ES CONSECUTIVO A -3/5


Antonio Silvio Palmitano
el 6/11/16a) Observa que -5 está comprendido entre -6 y - 3 (buscamos dos números enteros múltiplos del denominador 3, que sean múltiplos consecutivos), por lo tanto tienes que:
-6 < -5 < -3, luego dividimos en los tres miembros de la doble desigualdad por 3 y queda:
-2 < -5/3 < -1, por lo que tienes que el número entero que anteceda a -5/3 es -2.
b) Observa que -3 está comprendido entre -5 y 0 (buscamos dos números enteros múltiplos del denominador 5, que sean múltiplos consecutivos), por lo tanto tienes que:
-5 < -3 < 0, luego dividimos por 5 en los tres miembros de la doble desigualdad y queda:
-1 < -3/5 < 0, luego tines que el número entero consecutivo de -3/5 es 0.
Espero haberte ayudado.
-
-
Buenas noches. Si u y v son dos vectores linealmente independientes cómo puedo demostrar que u+v & u-v también lo son?


Antonio Silvio Palmitano
el 6/11/16Planteamos la combinación lineal nula para los vectores u+v y u-v ( ay b son números reales a determinar e indicamos al vector nulo con N):
a(u + v) + b(u - v) = N, distribuimos en los términos a la izquierda y queda:
au + av + bu - bv = N, ordenamos términos y queda:
au + bu + av - bv = N, extraemos factor común escalar por grupos y queda:
(a + b)u + (a - b)v = N, luego, como tienes que u y v son vectores linealmente independientes, tienes el sistema de ecuaciones:
a + b = 0, de donde despejas: b = -a (*)
a - b = 0,
luego reemplazas la expresión señalada (*) en la segunda ecuación y queda:
a - (-a) = 0, resuelves a la izquierda y queda: 2a = 0, multiplicas en ambos miembros por 1/2 y llegas a: a = 0,
luego reemplazas en la ecuación señalada (*) y queda: b = - 0, de donde tienes: b = 0.
Por lo que resulta que los vectores u+v y u-v son linealmente independientes.
Espero haberte ayudado.