-
Holaa unicoos!
Alguien me explica porque elnx= x ???
muchas gracias!


Antonio Silvio Palmitano
el 6/11/16Recuerda la función exponencial, cuya expresión es: f(x) = e^x, cuyo dominio es Df = R, y su imagen es If = (0,+inf).
Luego, su función inversa es la función logarítmica natura, cuya expresión es: g(x) = lnx, cuyo dominio es: Dg = (0,+inf), y su imagen es If = R.
Luego, como la composición de funciones inversas entre si es igual a la función identidad tienes:
a) e^lnx = x, con x ∈ (0,+inf).
b) ln(e^x) = x, con x ∈ R.
Espero haberte ayudado.
-
alguien me puede ayudar? llevo un rato dándole vueltas u no entiendo ni como dibujar el triangulo.
gracias


Antonio Silvio Palmitano
el 6/11/16Vamos con una orientación.
Dibuja un segmento de longitud 10, con un extremo en el origen de coordenadas, y el otro extremos en un punto del primer cuadrante, con ordenada y = 8.
El eje OX coincide con la línea de nivel de tierra, el eje OY es perpendicular y señala la altura del globo con respecto al nivel de tierra, y los extremos del segmento son los puntos de coordenadas O(0,0) y P(x,8), y tienes que |OP| = 10.
Luego, si llamas θ al ángulo determinado por el segmento OP y el semieje OX positivo, tienes:
senθ = 8/10, que al componer con la función inversa del seno queda: θ = 53,13° aproximadamente.
Observa que la longitud de la cuerda está representada por el segmento OP, y que los lados del triángulo son:
hipotenusa: OP, altura: segmento paralelo a OY trazado desde el punto P hasta cortar al eje OX, base: segmento con extremos en este último punto y el punto O(0,0):
Espero haberte ayudado.
-
Buenas a todos, un saludo cordial, debo realizar un diagrama de venn con el siguiente enunciado, alguien me ayuda?
El enunciado es el siguiente:
Todo Espacio Vectorial consta de cantidades vectoriales y escalares.
En el curso de Álgebra Lineal todos los enunciados son de Espacios Vectoriales.
En el curso de Álgebra Lineal todos los enunciados constan de cantidades vectoriales y escalares.
-
hola alguien me puede ayudar? el ejercicio dice: demuestra las siguientes identidades trigonométricas:
f) (cos∝- cosβ)²+(sen∝+senβ)²=4(sen²∝+β)/ (2)
he estado intentando usar las formulas de transformaciones de sumas en productos pero no se como seguir . tambien he intentado usar las identidades notables pero tampoco se como continuar. ¿alguien me ayuda? gracias
-
¡Hola!
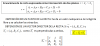
Tengo dudas con este ejercicio de matrices, no sé cómo plantearlo. Cualquier ayuda es muy muy bienvenida :) El ejercicio dice así: encuentre la matriz A y los vectores x y b tales que el sistema representado por la siguiente matriz aumentada se escriba de la forma Ax = b; además resuelve el sistema
2 0 0 | 3
0 4 0 | 5
0 0 -5 | 2
¡¡Muchas gracias de antemano!! :)
-


Antonio Silvio Palmitano
el 6/11/161) Planteamos las derivadas hasta el orden cuatro, y las evaluamos para el centro de desarrollo a = 0:
f(x) = (1+x)^(1/2), con f(0) = 1
f ' (x) = (1/2)(1+x)^(-1/2), con f ' (0) = 1/2
f ' ' (x) = (-1/4)(1+x)^(-3/2), con f ' ' (0) = -1/4
f ' ' ' (x) = (3/8)(1+x)^(-5/2), con f ' ' ' (0) = 3/8
f ' ' ' ' (x) = (-15/16)(1+x)^(-7/2), con f ' ' ' ' (0) = -15/16
Luego planteamos la expresión del polinomio de Taylor de orden 4, con centro de desarrollo a = 0 y queda:
P(x) = 1 + (1/2)x - (1 / 4*2!)x^2 + (3 / 8*3!)x^3 - (15 / 16*4! )x^4, resolvemos coeficientes y queda:
P(x) = 1 + (1/2)x - (1/8)x^2 + (1/16)x^3 - (5/128)x^4.
b) Tenemos la función cuya expresión es: f(x) = x/(1+x) = ( (1+x) - 1 )/(1+x) = distribuimos el denominador = 1 - 1/(1+x) = 1 - (1+x)^(-1), con centro de desarrollo: a = 1.
Luego planteamos las derivadas hasta el orden 4, y las evaluamos para el centro de desarrollo:
f(x) = 1 - (1+x)^(-1), con f(1) = 1 - 1/2 = 1/2
f ' (x) = (1+x)^(-2), con f ' (1) = 1/4
f ' ' (x) = -2(1+x)^(-3), con f ' ' (1) = -1/4
f ' ' '(x) = 6(1+x)^(-4), con f ' ' ' (1) = 3/8
f ' ' ' ' (x) = -24(1+x)^(-5), con f ' ' ' ' (1) = -3/4
Luego planteamos el polinomio de Taylor de orden 4 con centro de desarrollo a = 1 y queda:
P(x) = 1/2 + (1/4)(x - 1) - (1 / 4*2! )(x - 1)^2 + (3 / 8*3! )(x - 1)^3 - (3 / 4*4! )(x - 1)^4, resolvemos coeficientes y queda:
P(x) = 1/2 + (1/4)(x - 1) - (1/8 )(x - 1)^2 + (1/16)(x - 1)^3 - (1/32)(x - 1)^4.
Espero haberte ayudado.
-
Necesito ayuda con estos dos ejercicios de operaciones de vectores de 1ºBACH:
- Encuentra dos puntos P y Q pertenecientes a la recta r: 2x-3y+6=0. Comprueba que PQ es perpendicular a (2, -3). Escribe las ecuaciones paramétricas de r.
- Describe cómo son las rectas de las ecuaciones
a) x-2=0
b) y-3=0


Antonio Silvio Palmitano
el 6/11/16Puedes comenzar con asignar dos valores distintos a x, por ejemplo: 0 y 3:
para x1 = 0, reemplazas y tienes: -3y + 6 = 0, de donde puedes despejar: y = 2, por lo que tienes el primer punto de la recta: P(0,2);
para x2 = 3, reemplazas y tienes: 6 - 3y + 6 = 0, de donde puedes despejar: y = 4, por lo que tienes el segundo punto de la recta: Q(3,4);
luego, planteamos las componentes del vector u = PQ:
u = < 3-0, 4-2 > = < 3 , 2 >, luego planteamos el producto escalar entre el vector u y el vector del enunciado: v = < 2 , -3 >:
u o v = < 3 , 2 > o < 2 , -3 > = 3*2 + 2*(-3) = 6 - 6 = 0, y por la condición de perpendicularidad entre vectores no nulos, tenemos que u ⊥ v.
Luego, para plantear las ecuaciones cartesianas paramétricas de la recta r, tomamos uno de sus puntos y su vector director u (observa que u es un vector cuyas componentes hemos calculado a partir de los puntos P y Q que pertenecen a la recta), por lo tanto quedan:
x = 0 + 3t
y = 2 + 2t
con t ∈ R.
a) Despejas y queda: x = 2 (observa que y está "libre"), por lo que es la ecuación de una recta paralela al eje de ordenadas OY, que corta al eje OX en el punto de coordenadas: A(2,0).
b) Despejas y queda. y = 3 (observa que x está "libre"), por lo que es la ecuación de una recta paralela al eje de abscisas OX, que corta al eje OY en el punto de coordenadas: B(0,3).
Espero haberte ayudado.