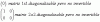-
denotamos y=y(t) el tamaño de una población en el tiempo t.
a) Cuál sería su ecuación diferencial?
b) Supón que cada unidad de tiempo se suprime 1/3 de la población existente. Cuál sería la ecuación que modele la nueva situación?


Breaking Vlad
el 27/1/20se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)
-
-
denotamos y=y(t) el tamaño de una población en el tiempo t.
a) Cuál sería su ecuación diferencial?
b) Supón que cada unidad de tiempo se suprime 1/3 de la población existente. Cuál sería la ecuación que modele la nueva situación?


Breaking Vlad
el 27/1/20se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)
-
Hola alguien puede darme un ejemplo de una matriz diagonalizable que no sea invertible?
-


Jose Ramos
el 26/1/20Veo que tienes dificultad para resolver estos ejercicios utilizando planos. Pues no los hagas así. Hazlos con la técnica del punto genérico sobre una recta como hice el anterior.
La recta r que contiene a C y D es paralela a la recta que contiene A y B (ABCD forman un rectángulo). Como r pasa por (0,0,0) sus paramétricas son x = λ, y = λ, z = λ. El punto D que busco está en esa recta, entonces D = ( λ, λ, λ). Además AD es perpendicular al vector de r, dr=(1,1,1)
AD.dr = 0, entonces ( λ-1, λ-1, λ).(1,1,1)=0 , λ-1+ λ-1+ λ=0, λ =2/3. El punto D es (2/3, 2/3, 2/3)
-


Jose Ramos
el 26/1/20El tal plano lo construye para resolver el ejercicio. Lo resuelve con ese plano auxiliar. Lo que hace es buscar el plano que pasa por Q y es perpendicular a r. Este plano corta a r en un punto R. La recta pedida es la que pasa por Q y R.
Hay otra forma de hacerlo: Sabes dos cosas por el enunciado de la recta que buscas: corta a r en un punto R, y es perpendicular a r.
El punto R está en r, entonces tiene de coordenadas ( pasas r a paramétricas) las paramétricas de r. Construyes el vector QR con el parámetro y como QR y vr son perpendiculares, con el producto escalar = 0, despejas el parámetro, obteniendo el punto R. Te lo envío hecho, pero antes inténtalo tú.