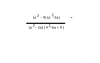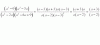Foro de preguntas y respuestas de Matemáticas

Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.

Ir a beUnicoos

Joship
el 27/10/16

Queria pedir ayuda con esta probabilidad no me hallo

••0 voto/s
•
Antonio Silvio Palmitano
el 27/10/16
Observa que en la primer elección puede tomar a cualquier esclavo, por lo que la probabilidad es 10/10. Una vez elegido un esclavo, la probabilidad de escogerlo en la segunda elección es 1/10, y la probabilidad de volver a elegirlo en la tercera elección es 1/10. Por lo tanto, la probabilidad de elegir siempre al mismo de los diez esclavos es, por el principio de multiplicación (observa que las elecciones son independientes entre si, ya que una elección no influye sobre la siguiente):
N = 10/10 * 1/10 * 1/10 = 10/1000 = 1/100.
Espero haberte ayudado.

•0 voto/s
•

Cancelar
Angel
el 27/10/16

3. Juan hoy hace 45 años y trabaja en el sector bancario. Ante las noticias de EREs en este sector, quiere planificar su futuro ahorrando para no sufrir problemas financieros cuando llegue la jubilación. Parte de los siguientes parámetros:

• Tiene ahorrados € 45.000 en una cuenta de ahorro y no tiene deudas.
• Estima que se prejubilará a los 61 años y que vivirá hasta los 90 años.
• Los ahorros de los que dispone cree que los puede rentabilizar en una cuenta de ahorro a un tipo de interés promedio del 4,5% nominal capitalizable mensualmente durante los años en que está activo ya un 2% nominal capitalizable mensualmente durante el plazo en que ya disfrutará de la jubilación.

3.1 Calcular qué aportación constante deberá hacer cada principio de mes en la cuenta de ahorro que tiene abierto, y hasta el momento en que se prejubilará, para conseguir tener una prestación mensual de 1.000 €, al final de cada mes, durante su jubilación. Los 45.000 € que Juan tiene ahorrados también ingresan hoy en esta cuenta de ahorro.

entiendo que podemos hacerlo así:

X*0.0016=1000 --> x=625000
0.02/12=0.0016

[c·(1-(1+0.00375)^(-192))/0.00375][(1+0.00375)^192 ]=(625000-45000)= 2068.14

es correcto? o se refiere a que quiere gastarse todo lo ahorrado hasta la jubilación para que le quede 1000 cada mes hasta los 90?

gracias.

••0 voto/s
•
David
el 28/10/16
Lo siento de corazón pero tu duda es de Economía o matemáticas financieras y carezco de conocimientos para ayudarte. Espero lo entiendas. Un abrazo!

•1 voto/s
•
Angel
el 28/10/16
gracias igualmente!

•0 voto/s
•

Cancelar
raul garcia
el 27/10/16

como se hacen operaciones con potencias y en la misma operacion potencias de base10

••1 voto/s
•
:)
el 27/10/16
https://www.youtube.com/watch?v=OEQdiXe_lkQ

•0 voto/s
•

Cancelar
Jonathan Torres
el 27/10/16

Quien Me Responde Este Enunciado.

••0 voto/s
•
César
el 27/10/16
VA Jonathan

•1 voto/s
•

Cancelar
:)
el 27/10/16

hola tengo una duda q ya no se como explicarle a una compañera segun ella
0.1 a 0.5 no es 0
alguno me ayuda

••0 voto/s
•
César
el 27/10/16
Pues primero explícate tú un poco . no entiendo la pregunta.

•0 voto/s
•
:)
el 27/10/16
cesar desde el cel me complica pero ahora ella considera que un cero con coma asi sea 0,1 ya no es cero y le dije preguntamos y vemos que nos dicen muchas gracias

•0 voto/s
•
César
el 27/10/16
Pues desde luego 0,1 no es cero aunque este cerca de él. Si tomas la parte entera de 0,1 si, recuerda que 0,1=1/10 que no es cero.
No se si te ayudé. :-)

•0 voto/s
•
:)
el 27/10/16
gracias el tema es xq estamos hallando raiz en ecuaciones de segundo grado y al verificar nos da 0.2 y 0.15.... entonces no sabiamos si era raiz o no muchas gracias

•0 voto/s
•

Cancelar
Matias
el 27/10/16

Hola Unicoos. Me pueden decir si resolvi bien el ejercicio? y quisiera saber que quiere decir con "indicando la base", como se esto?. Gracias!

••0 voto/s
•
Antonius Benedictus
el 27/10/16
Creo que está bien, Matías, especificando base de entrada y de salida (la canónica).

•0 voto/s
•

Cancelar
sus
el 27/10/16

Hola unicoos. Necesito ayudo! como despejo la X en esta ecuación matricial? AX+X^t= B GRACIAS

••0 voto/s
•
Antonius Benedictus
el 27/10/16
La ayuda, SUS:

•1 voto/s
•
sus
el 27/10/16
Y cómo sería el cálculo de tI con una matriz? Porque la matriz traspuesta de la inversa coincide con su mismo valor.

•1 voto/s
•
Antonius Benedictus
el 27/10/16
Entendí X·t , no traspuesta. Lo siento.

•0 voto/s
•
Antonius Benedictus
el 27/10/16
Solo se me ocurre asignar incógnitas a los elementos de X, operar, igualar e intentar resolver el sistema lineal resultante.

•1 voto/s
•
sus
el 28/10/16
Genial eso fue lo q pemsé en un primer momento. Muchas gracias

•0 voto/s
•

Cancelar
Infinity 4K
el 27/10/16

hola unicoos como están? Necesito ayuda con este ejercicio, que es un ejercicio de examen, espero que me.puedan ayudar . Gracias

••0 voto/s
•
Antonius Benedictus
el 27/10/16
Gracias, Antonio. Ya retiré el cálculo equivocado. Muchos ojos siempre ven más y mejor.

•3 voto/s
•
Infinity 4K
el 28/10/16
muchas gracias por tu ayuda, me sirvió de mucho

•0 voto/s
•

Cancelar
raul garcia
el 27/10/16

Tambien tengo este enunciado calcula la raiz y el resto si tiene

••0 voto/s
•

Cancelar