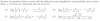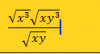-
Alguien me puede ayudar con esta ecuación? Es que, no llevo muy bien las ecuaciones con dos incógnitas:
[(24 · 79) / 100] + [(25 · x) / 100] + [(26 · y) / 100] = 24,31
Muchas gracias!!


Antonio Silvio Palmitano
el 27/10/16Observa que puedes multiplicar por 100 en todos los términos y queda:
24*79 + 125x + 26y = 2431, luego resuelves el primer término de la izquierda y queda:
1896 + 125x + 26y = 2431, luego haces pasaje de término y queda:
125x + 26y = 2431 - 1896, resolvemos a la derecha y queda:
125x + 26y = 535.
Luego, debes ver si necesitas despejar x o despejar y, si es que la ecuación forma parte del planteo de un problema.
Espero haberte ayudado.
-
alguien me puede explicar como se resuleven los sistemas de ecuaciones?
cosx-seny=0
cosx+sen^2y= 3/4


Antonio Silvio Palmitano
el 27/10/16Puedes proponer las sustituciones (cambios de incógnitas):
u = cosx, w = seny (obsrva que u y w deben tomar valores comprendidos entre -1 y 1), luego sustituyes y el sistema de ecuaciones queda:
u - w = 0, de donde tienes: u = w (*),
u + w^2 = 3/4.
luego sustituyes la expresión señalada (*) en la segunda ecuación y queda:
w + w^2 = 3/4, haces pasaje de término, ordenas términos y queda:
w^2 + w - 3/4 = 0, que es una ecuación polinómica cuadrática, aplicas la fórmula resolvente y quedan las soluciones:
a) w = - 3/2 (observa que es absurda según la sustitución w = seny),
b) w = 1/2,
luego, reemplazas en la ecuación señalada (*) y tienes:
u = 1/2.
Luego, a partir de las sustituciones que hemos propuesto, tenemos:
u = cosx = 1/2, que nos conduce a: x1 = 60° = pi/3, x2 = 300° = 5pi/3;
w = seny = 1/2, que nos conduce a: w1 = 30° = pi/6, w2 = 150° = 5pi/6.
Por lo tanto las soluciones (x,y) son:
( pi/3 , pi/6 ), ( pi/3 , 5pi/6 ), (5pi/3, pi/6), (5pi/3,5pi/6).
Espero haberte ayudado.
-
alguien me puede ayudar con esta identidad o decirme que pasos tengo que seguir?
cos (a-b) - cos (a+b)/ sen (a+b) + sen (a-b)
Gracias.


Antonio Silvio Palmitano
el 27/10/16Puedes comenzar por desarrollar el numerador (N) y el denominador (D) por separado, hasta reducirlos a sus mínimas expresiones:
N = cos(a-b) - cos(a+b) = aplicamos identidades del coseno de la resta y de la suma de dos ángulos:
= cosa*cosb + sena*senb - (cosa*cosb - sena*senb) = distribuimos el signo en el agrupamiento:
= cosa*cosb + sena*senb - cosa*cosb + sena*senb = cancelamos términos opuestos y reducimos términos semejantes:
= 2sena*senb.
D = sen(a+b) + sen(a-b) = aplicamos identidades del seno de la suma y de la resta de dos ángulos:
= sena*cosb + cosa*senb + sena*cosb - cosa*senb = cancelamos términos opuestos y reducimos términos semejantes:
= 2sena*cosb
Luego, sustituimos en la expresión y queda:
N/D = 2sena*senb / 2sena*cosb = simplificamos = senb/cosb = tanb.
Espero haberte ayudado.
-
-
Hola alguien puede explicarme como calcular este ejercicio con los pasos. Muchas gracias de antemano:


Antonio Silvio Palmitano
el 27/10/16Observa que tienes producto y división entre raíces cuadradas, por lo que puedes asociar y queda:
V( x^3 * xy^3 / xy ) = simplificas los factores x, y aplicas propiedad de la división de potencias con bases iguales para y:
= V( x^3 * y^2 ) = descompones el factor x^3 en factores con exponentes menores:
= V( x * x^2 * y^2 ) = distribuyes la raíz entre los factores:
= V(x) * V(x^2) * V(y^2) = simplificas índices y exponentes en los dos últimos factores:
= V(x) * x * y = xyV(x).
Espero haberte ayudado.

Mélany
el 27/10/16
Hola Laura. Pues esa operación se resuelve así, racionalizando. De hecho, tienes videos de únicos que te lo explican:- Primero tienes que quitar el denominador. El denominador, cuando hay una raiz cuadrada, se quita poniendo la misma raiz cuadrada que multiplique en una fracción a la fracción que tu tienes. Por ejemplo, en este caso se haría: [(√x3√xy3) / √xy] · (√xy / √xy). Así, quitarías el denominador y se quedaría así: (√xy3√x3√xy) / xy.
- A partir de aquí, ya solo tienes que simplificar: √x5y4 / xy → y2x2 · (√x / xy)
Creo que se quedaría así. De todas formas y como ya he mencionado antes, tienes unos videos de radicales que te explican como hacer todo esto. Un saludo!!
-
Buen día,
Solicito ayuda con este ejercicio.
Pruebe que la ecuación del plano que pasa por el origen y la linea de intersección de los planos:
3x- y 2z -4 = 0
es el plano x + 5y + 2z = 0
x + y + z ‐1 = 0
Mil gracias


Antonio Silvio Palmitano
el 27/10/16Puedes plantear el vector director de la recta intersección entre los planos. como el producto vectorial de sus vectores normales:
u = <3,-1.2> x <1,1,1> = <-3,-1,4>;
luego puedes determinar uno de sus puntos, asignando un valor arbitrario a una de las variables, por ejemplo x = 0, y resolver el sistema que queda entre las ecuaciones de los planos que determinan la recta:
- y + 2z = 4
y + z = 1
resuelves el sistema y tienes y = -2/3, z = 5/3, por lo que el punto de la recta queda: A(0,-2/3,5/3)
Luego, puedes plantear al vector normal del plano buscado como el producto vectorial entre el vector director de la recta y el vector que uno los puntos O(0,0,0) que pertenece al plano buscado, y A que pertenece a la recta, y queda:
n = <-3,-1,4> x <0,-2/3,5/3> = <1,5,2>.
Luego, la ecuación cartesiana implícita del plano buscado queda (observa que como pasa por el origen de coordenadas tendrá término independiente igual a cero), queda:
1x + 5y + 2z + 0 = 0, que puede escribirse:
x + 5y + 2z = 0.
Espero haberte ayudado.
-
Hola,
En el ejercicio 1 creo que es contínua,
no está acotada superiormente...ya que f(3+) tiende a infinito
no contradice ningún teorema...ya que, aunque el teorema de Weierstrass dice que las funciones continuas en [a,b] están acotadas, nuestro intervalo es abierto (a,b)
¿me equivoco?
El ejercicio 2 no se como hacerlo, ¿alguien me podría ayudar?
Gracias