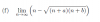-
Lucia Napoli
el 17/10/16Hola, en este ejercicio me piden hallar la ecuacion de la recta tangente y normal al grafico de una funcion expresada en forma implicita en el punto (0,1). ¿Esta bien hecho asi? ¿A que se refiere con normal?
Antonio Silvio Palmitano
el 17/10/16Debes corregir el paso de la derivación implícita. Tenemos la ecuación:
y*x^4 + e^x * y^3 = 1, luego derivamos con respecto a x (observa que tenemos producto en cada término):
y ' * x^4 + y * 4x^3 + e^x * y^3 + e^x * 3y^2 * y ' = 0, hacemos pasajes de términos:
y ' * x^4 + e^x * 3y^2 * y ' = - y * 4x^3 - e^x * y^3, extraemos factor común a la izquierda:
y ' * ( x^4 + e^x * 3y^2 ) = - y * 4x^3 - e^x * y^3, hacemos pasaje de factor como divisor y llegamos a:
y ' = ( - y * 4x^3 - e^x * y^3 ) / ( x^4 + e^x * 3y^2 ), con la condición: x^4 + e^x * 3y^2 distinto de 0.
Luego, evaluamos para el punto Po(0,1) y tenemos: y ' = -1/3.
Luego, para la recta tangente tienes la ecuación:
y - 1 = (-1/3)*(x - 0).
Luego, para la recta normal, que es perpendicular a a la recta tangente (recuerda la condición de perpendicularidad entre rectas), tienes la ecuación:
y - 1 = 3*(x - 0).
Espero haberte ayudado.
-
Axel Morales Piñón.
el 17/10/16Algo básico, no me cuadran mis soluciones con las del ejercicio):
Axel Morales Piñón.
el 17/10/16Lo sé amigo Antonio, pero no lo incluí por lo que para el dominio de la función el denominador tiene que ser mayor o distinto de cero, en mi solucionario, en este ejercicio trae como
solución los 3 intervalos que puesto a probar, en los dos últimos va bien pero, en el primero queda con signo negativo:/
Antonio Silvio Palmitano
el 17/10/16Observa que si se trata de plantear el dominio de la función, ya lo tienes resuelto.
Pero, si se trata del signo de los valores de la función, ahí debes agregar un nuevo punto de corte como indica el colega Antonio, x = 1/3 (observa que pertenece al dominio y que para él la función toma el valor cero), y subidvidir el intervalo al que pertenece.
Espero haberte ayudado
-
Sofía
el 17/10/16Hola unicoos! Necesito ayuda con este ejercicio.
Las posiciones del movimiento de una nave espacial vienen identificados por los siguientes vectores: Ā = (3 i – 4 j + 4 k) y Ē = (2 i + 3 j – 7 k). Determinar:
a) el valor numérico de los vectores definidos como: C = (Ā + Ē) y D = (2 Ā – Ē).
b) Exprese los vectores C y D en función de sus componentes rectangulares.-
No entiendo por qué los vectores son 3i o 4j.. osea, un numero acompañado de una letra.
Gracias!
-
Adrhian Robles
el 17/10/16 -
Sergio Suarique
el 17/10/16¿Me podrían ayudar con esta integral?
a
Sergio Suarique
el 17/10/16 -
Maria del castillo
el 17/10/16
me podéis resolver este limite de sucesiones? gracias!
Antonio Silvio Palmitano
el 17/10/16Debes comenzar por multiplicar y dividir por la expresión "conjugada", ya que el límite es indeterminado, lo haces y, luego de distribuir y simplificar, queda:
Numerador = N = n^2 - (n+a)(n+b) = distribuyes = n^2 - n^2 - an - bn - ab = n(-a - b - ab/n)
Denominador = D = n + V( n^2 * (1 + a/n)*(1 + b/N) ) = n + V(n^2)*V( (1 + a/n)*(1 + b/n) ) = n + n*V( (1 + a/n)*(1 + b/n) ) = n*( 1 + .V( (1 + a/n)*(1 + b/n) ) )
Luego, la expresión, luego de simplificar los factores n, queda: N/D = (-a - b - ab/n)/( 1 + V( (1 + a/n)*(1 + b/n) ).
Luego, pasamos al cálculo del límite:
Lím(x-->+inf) (- a - b - ab/n)/( 1 + V( (1 + a/n)*(1 + b/n) ) ) = (- a - b)/( 1 + V(1*1) = (-a -b)/(1 + 1) = (- a - b)/2.
Espero haberte ayudado.
-
dovigame
el 17/10/16
Profe mira lo intente por el método de ecuación oracional para obtener los intervalos con los que hacemos la evaluación y me resultó una ecuación de tercer grado no se si se puede obtener los vértices de este modo.Y otra cosa quisiera ayudar a los demás y no sé como responder a sus dudas por favor enseame odime donde escribo
David
el 18/10/16¿ecuación oracional? ¿vertices en una ecuación de tercer grado? ¿¿??... ¿Nos dejas una foto con el enunciado LITERAL y tu duda exacta?
En cuanto a ayudarnos en los foros, sería genial. Basta con que pulses el boton azul con la flechita en la pregunta que quieras de los foros y que dejes tu respuesta. Un abrazo! -
lbp_14
el 17/10/16Hola Unicoos sigo cometiendo errores en este tipo de operaciones, y esta vez también, podrían ayudame?
Muchísimas gracias
Antonio Silvio Palmitano
el 17/10/16Observa el primer agrupamiento:
1/(1+x) + 2x/(1 - x^2) = factorizamos el denominador del segundo término = 1/(1+x) + 2x/( (1+x)(1-x) ) = extraemos denominador común:
= ( 1*(1-x) + 2x*1 ) / ( (1+x)(1-x) ) = ( 1 - x + 2x ) / ( (1+x)(1-x) ) = (1+x) / ( (1+x)(1-x) ) = simplificamos = 1/(1-x)
El segundo agrupamiento lo resolviste bien. Luego, vamos con el producto de agrupamientos:
1/(1-x) * (1-x)/x = 1*(1-x) / ( (1-x)*x ) = simplificamos = 1/x.
Espero haberte ayudado.
-
Jordi García
el 17/10/16
