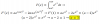Lo primero es que esboces ambas graficas. Se supone que sabes representar y=senx e y=sen(2x)...
Lo siguiente es que obtengas los puntos de intersección entre ambas, resolviendo la ecuacion senx=sen(2x)... senx=2senx.cosx... Tienes una identica...

Sí, por ese teorema y ,ojo, la regla de la cadena:

Una precisión de cálculo: cuando evaluamos la derivada de la función queda:

F ' (1) = a*e^(a^2) - 2a*e^(a^2) = - a*e^(a^2).

Luego tenemos:

- a*e^(a^2) = e^(a^2), luego:

- a*e^(a^2) - e^(a^2) = 0, luego:

e^(a^2) * (- a - 1) = 0, luego (observamos que e^(a^2) > 0):

- a - 1 = 0, y finalmente:

-1 = a.

Espero haber ayudado.

Va, Nacho:

Observa que puedes aplicar el Teorema Fundamental del Cálculo Integral y tienes: F ' (x) = 3*e^(- x^2 + 4) (*).

Luego, observa en la expresión de la función F(x), que el argumento de la integral es estrictamente positivo, por lo tanto para que tengamos F(x) = 0 x debe tomara el valor 2, ya que quedaría F(2) definida con una integral entre 2 y 2, que es igual a 0.

Luego, para la función inversa tenemos: F^(-1) (y) = x, y si y = 0 tenemos que x = 2.

Luego, has visto en clase cuál es la relación entre la derivada de una función y la derivada de su inversa: F^(-1) ' (y) = 1 / F ' (x),

por lo que tenemos para nuestro ejercicio:

F^(-1) ' (0) = 1 / F ´(2) (**)

luego, a partir de la ecuación señalada (*) tenemos que: F ' (2) = 3*e^(- 2^2 + 4) = 3*e^0 = 3*1 = 3.

Por último, reemplazamos en la igualdad señalada (**) y llegamos a:

F^(-1) ' (0) = 1 / F ´(2) = 1/3.

Espero haberte ayudado.

Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. Lo siento de corazón… Espero lo entiendas

Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas (tu duda se da en LOGICA)... Lo siento de corazón… Espero lo entiendas

 Ahí te va el apartado a), está "analizado" utilizando cálculo lógico que es más rápido....pero si te dejan con tablas de verdad más fácil aún, aunque te lleva más tiempo 

A continuación llegamos a la conclusión a partir de las premisas (P1 y P2) simbolizando cada forma enunciatica con las consonantes p,q y r:

Simbolización

p= Bernardo se casa

q= Florinda se suicida

r= Bernardo se hace monje 

Formalización

(1) p --->q          P1

(2) q <---> ¬r     P2

(3) (q ---> ¬r) ^ (¬r ---> q)              (Eliminación del coimplicador) 2

(4) q---> ¬r                                       (Eliminación de la disyunción) 3 

(5) p---> ¬r       Conclusión             (Silogismo) 1,4

No puedo ayudarte con tu duda, lo siento...  Unicoos por ahora se queda en bachiller... 

Si la función a integrar con respecto a x es: f(x) = 3*cos(n*pi*x/5), puedes aplicar la sustitución (cambio de variable):

w = n*pi*x/5, de donde tienes: dw = n*pi*dx/5, de donde también tienes: ( 5/(n*pi) )*dw = dx, luego sustituyes y la integral queda:

I = 3 * ( 5/(n*pi) ) * Integral( cosw*dw ) = ( 15/(n*pi) ) * senw + C = ( 15/(n*pi) ) * sen(n*pi*x/5) + C.

Si la expresión de la función a integrar es otra, por favor vuelve a consultar.

Espero haberte ayudado.

Antonio, esa es la función a integrar. ¿Te molestaría hacerlo en papel?

Si eres un experto y puedes hacerla por partes, lo preferiría que lo hicieras así porque me familiarizo más con esa forma de integrar.

Yo utilizo el manual de Schaum para esas integrales pero no la encuentro.

Muchas gracias.

Una observación importante: en este ejercicio tratas con una integral que se resuelve por sustitución, pero no se resuelve por partes.

Luego te envío el ejercicio en foto, tal como pides o, llegado el caso, alguno de los colegas lo hará.

Podrías buscar aquí:
http://www.unicoos.com/cursos/1-eso/matematicas

Si tienes un ejercicio concreto que no puedes hacer lo mandas.

Hice el a y c. Si puedes ampliar la foto para hacer el resto. Creo que estoy medio ciego jaja.