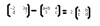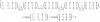-
Hola, buenas tardes. Estoy trabajando con una serie de ejercicios de ejercicios usando resolución proposicional y determinando cuales son deducciones válidas; ya realicé 2:
La primera con tabla de verdad y la segunda teniendo en cuenta que una implicación A -> B sólo es falsa si B es FALSO y A es VERDADERO, luego suponiendo que ¬r es FALSO y siguiendo una serie de procedimientos.
Ahora, sólo se hacerlo de esos dos métodos, pero cómo puedo hacer esta otra:

Cómo puedo determinar si es válida mediante algún método de resolución que no sea los que ya he utilizado?
Gracias de antemano.


Antonio Silvio Palmitano
el 11/10/16Observa que tienes tres premisas, las que deben ser verdaderas (indicamos conjunción con "y", y disyunción con "o"):
P1: (p-->q) y r
P2: s-->k
P3: r-->s
Observa que P1 es Verdadera, por lo que resulta: (p-->q) es Verdadera y también r es Verdadera.
Luego, como P3 es Verdadera, y como ya tenemos que r es Verdadera, tenemos que s también es Verdadera:
Luego, como P2 es verdadera, y como ya tenemos que s es Verdadera, tenemos que k también es Verdadera (*).
Luego, pasamos a la conclusión (observa que es una disyunción, por lo que es falsa únicamente si ambas proposiciones atómicas son falsas).
C: q o k, y como sabemos (*) que k es verdadera, la conclusión resulta verdadera independientemente del valor de verdad de la proposición q.
Espero haberte ayudado.
-
Una consulta.Para sacar puntos de inflexion de una funcion, tendria que igualar la segunda derivada de dicha funcion a 0.Y de ahi con los valores obtenidos verificar la concavidad, y donde cambia la curvatura..para saber si son o no puntos de inflexion.Si es correcto esto, que pasa si por ejemplo al igualar la segunda derivada a 0, no existen valores de x.Osea me explico mejor...Tengo como segunda derivada y=e^x .(-x^2 -2x-2) e a la equis por el parentesis..Bueno al igualar a 0, me queda la ecuacion de segundo grado, y al hacer bascara la raiz me queda negativa, por lo que no puedo sacar valores de x.Mi duda es, en ese caso no habria puntos de inflexion? o estoy omitiendo algo?


Antonio Silvio Palmitano
el 11/10/16Primero verifica que no haya error en todo el proceso hasta llegar a la expresión de la derivada segunda. Asumiendo que la expresión es la que has escrito, observa que se trata de una función continua en R y, por lo tanto, al no obtener raíces reales puedes concluir que si gráfica no presenta puntos de inflexión.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 11/10/16Planteamos (observa que el argumento de la expresión de g es una expresión poliónica, cuyo límite es igual a cero cuando x tiende a cero por derecha o por izquierda):
a) Lím(x-->0+) g(x^3 - x) = aplicamos propiedad del límite de una función continua por derecha = g( Lím(x-->0+)(x^3 - x) ) = g(0) = 4.
b) Lím(x-->0-) g(x^3 - x) = aplicamos propiedad del límite de una función continua por izquierda = g( Lím(x-->0-)(x^3 - x) ) = g(0) = 7.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 11/10/16a) Indicamos raíz quinta con (5V). Intentaremos ver si w^5 y w1^5 nos conducen al mismo resultado z.
Observa que el número complejo w tiene módulo 4 y argumento t = 2pi/7, y su expresión en forma polar queda: w =(4)(2pi/7).
Observa que el número complejo w1 es el producto de w por otro complejo con módulo 1 y argumento 2pi/3, luego, efectuamos el producto (recuerda que se multiplican los módulos y se suman los argumentos) , tenemos entonces:
w1 = (4*1)(2pi/7 + 2p/3) = (4)(20pi/21)
Luego, planteamos las quintas potencias de ambos números complejos (recuerda que el módulo se eleva a la quinta, y que el argumento se multiplica por 5 y, de ser necesario, debe ser reducido al argumento principal):
w^5 = ( (4)(2pi/7) )^5 = (4^5)(5*2pi/7) = (1024)(10pi/7)
w1^5 = ( (4)(20pi/21) )^5 = (4^5)(5*20pi/21) = (1024)(100pi/21) = (1024)(4pi + 16pi/21) = tomamos argumento principal = (1024)(16pi/21)
Observa: si w y w1 fuesen ambas raíces quintas de un mismo número complejo, tendríamos que haber llegado al mismo módulo (como hemos llegado) y al mismo argumento principal, que no es este caso. Por lo tanto concluimos que el complejo w1 no es raíz quinta de z, como si lo es w según el enunciado.
b) Recuerda la relación entre la forma exponencial de Euler y la forma polar para un número complejo:
e^(a+bi) = e^a * e^bi = (e^a)(b), con b expresado en radianes, por lo tanto planteamos:
z = e^(2 + ipi/3) = (e^2)(pi/3) = expresamos en forma binómica = e^2 * ( cos(pi/3) + i*sen(pi/3)b) = reemplazamos valores =
= e^2 * ( 1/2 + (V(3)/2)i ) = distribuimos para expresar en forma cartesiana binómica = e^2 / 2 + (e^2)*(V(3)/2)i.
Luego tenemos:
parte real: Re(z) = e^2 / 2
parte imaginaria: Im(z) = (e^2)*(V(3)/2).
Espero haberte ayudado.
-
Hola buenas, nose Como aplicar el punto ll) y lll) no entiendo por que en la ecuación del Plano hay más de un vector


Pablo Reyes
el 10/10/16Te puedo ayudar con el apartado III:
Has de hacer un determinante 3x3: en la primera fila poner x y x
en la segunda fila el vector PQ y la tercera fila el vector PR
De esta forma de saldrá un plano con sus respectivas coordenadas x y z igualado a cero. Seguidamente sustituyes el punto ese que te piden en la ecuación del plano, si da cero, es que está en el plano, si no da cero, no está en él.


Antonio Silvio Palmitano
el 10/10/16Observa en que la ecuación vectorial paramétrica del plano del ejercicio II.
si evalúas para t=1 y k=0, obtienes: (x,y,z) = (-1,1,1), que son las componentes del vector posición para el punto Q;
si evalúas para t=0 y k=1, obtienes: (x,y,z) = (3,-1,1), que son las componentes del vector posición para el punto R;
si evalúas para t=0 y k=0, obtienes (x,y,z) = (1,0,2), que son las componentes del vector posición para el punto P;
por lo tanto tenemos que la proposición es verdadera.
Para el ejerccio III: evaluamos en la ecuación vectorial paramétrica del plano y queda:
(-3,2,1) = (1,0,2) + t(-2,1,-1) + k(2,-1,-1);
luego planteamos una ecuación para cada componente:
-3 = 1 - 2t + 2k
2 = 0 + t - k
1 = 2 - t - k
luego hacemos pasajes de términos, reducimos términos semejantes y el sistema queda:
2t - 2k = 4
-t + k = -2
t + k = 1, despejamos y queda: t = 1 - k (*), luego sustituimos en las dos primeras ecuaciones y quedaN:
2(1-k) - 2k = 4
-(1-k) + k = -2
distribuimos, hacemos pasajes de términos, reducimos términos semejantes y el sistema queda:
-4k = 2
2k = -1, despejamos y tenemos: k = -1/2, que se verifica en la primera ecuación,
luego, a partir de la ecuación señalada (*) tenemos: t = 1 - (-1/2) = 3/2.
Por último, como tenemos los valores para los parámetros t y k, concluimos que el punto pertenece al plano y que la proposición es verdadera.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 10/10/16Un camino altrenativo consiste en aplicar el Teorema del Resto, ya que el divisor es un binomio elemental: (x-4), y como nos pide que el polinomio (P(x))sea divisible, debemos plantear que el resto (R) es igual a cero, tal como dice el colega Enrique. Planteamos entonces:
P(4) = R, luego evaluamos:
4^5 - 8*4^2 + 4m - 6*4^3 + 1 = 0, resolvemos términos:
1024 - 128 + 4m - 384 + 1 = 0, reducimos términos semejantes:
4m + 513 = 0, despejamos y llegamos a:
m = - 513/4.
Espero haberte ayudado.
-