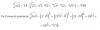-
DueFreitas
el 29/9/16 -
Javier
el 29/9/16 -
Jon buendia
el 29/9/16 -
Matías
el 29/9/16Me ayudan con el ejercicio 4? Gracias !!!
ISebastian Quintero
el 29/9/16 -
The punk
el 29/9/16Hola necesito su ayuda unicoos, yo demostré el apartado b pero esta mal y no entiendo como hacerlo bien, por favor necesito su ayuda....trate por contra-reciproco pero no me salio
-
Maria del castillo
el 29/9/16alguien me puede ayudar a factorizar X^4+1, en números complejos?
Gracias!!
Miguel Fuego
el 29/9/16Te doy un par de pistas, y si sigues teniendo problemas lo reintentamos de otra manera:
-Si despejamos x nos que que x es igual a la raíz cuadrada de i (no digo nada del signo)
-¿Cuántas soluciones tiene que tener la ecuación si es de grado cuarto?
-Si dibujas las soluciones en el plano complejo, los puntos serán los vértices de un polígono regular.
-Una expresión útil en análisis complejo es que i = e^((pi/2)* i)
¡Suerte!
Antonio Silvio Palmitano
el 29/9/16Observa que i^2 = -1, luego:
x^4 + 1 = x^4 - (-1) = (x^2)^2 - i^2 = diferencia de cuadrados = (x^2 + i)(x^2 - i) (*)
Luego, trabajamos cada factor por separado:
Observa que i = (1)(90°) en forma polar, y que sus raíces son:
x1 = (1)(45°) = en forma trigonométrica = cos45° + isen45° = en forma binómica = (V(2)/2)(1 + i)
x2 = (1)(225°) =en forma trigonométrica = cos225° + isen225° = en forma binómica = (V(2)/2)(-1 - i)
Observa que -i = (1)(270°) en forma polar, y que sus raíces son:
x3 = (1)(135°) = en forma trigonométrica = cos135° + isen135° = en forma binómica = (V(2)/2)(-1 + i)
x4 = (1)(315°) = en forma trigonométrica = cos315° + isen315° = en forma binómica = (V(2)/2)(1 - i).
Por último, continuamos la factorización que hemos interrumpido en la indicación (*) y queda:
x^4 + 1 = (x - x1)(x - x2)(x - x3)(x - x4).
Espero haberte ayudado.
-
Andrew
el 29/9/16Estudiar la monotonía de la función f(x)=x^3 en el punto de abscisa x=0
sé que para hacer la monotonía hay que hacer la derivada de x^3 y luego ya no sé seguir
César
el 29/9/16Andrew
el 29/9/16
Miguel Fuego
el 29/9/16Debes buscar en qué puntos se anula la derivada (pueden ser varios aunque en tu caso sólo hay uno). Cuando tienes esos puntos, digamos que sacaste que se anula para x = 1 y x = 2 (aunque no sea el caso, esto sólo es un ejemplo).
Para estudiar la monotonía necesitas ver qué signo tiene la derivada a ambos lados de los puntos en que se anula, es decir, a izquierda y derecha del 1, y a izquierda y derecha del 2. Por ejemplo puedes comprobar para los valores x= 0, x = 1,5, x= 3.
En tu función sólo tienes que comprobar el signo en dos puntos que estén a izquierda y derecha del punto en que se anula la primera derivada.
-
Rafa
el 29/9/16
- Sean los conjuntos A y B. Y Q={ VxW tq V∈P(A), W∈P(B)}. Demostrar si es cierta o falsa,la siguiente igualdad. P(AxB)=Q mmmm cuando se refiere a que Q es el producto cartesiano de VxW tal que V pertenece a las partes de A, quiere decir que V es un conjunto que forma parte de la coleccion de las partes de A?? Alguna resolucion?
-
Elena Wang
el 29/9/16Alguien me podría ayudar con estos dos ejercicios??!! Mil gracias!!
Antonio Silvio Palmitano
el 29/9/162) Observa que los argumentos de los logaritmos deben ser estrictamente positivos.
Hacemos pasaje de divisor como factor y la ecuación queda (indicamos logaritmo en base b como log):
log(16 - x^2) = 0, componemos con la función inversa del logaritmo en base b y queda:
16 - x^2 = b^0, resolvemos a la derecha y queda:
16 - x^2 = 1, hacemos pasaje de término, resolvemos a la derecha y queda:
-x^2 = - 15, multiplicamos por -1 en ambos miembros, hacemos pasaje de potencia como raíz y queda:
x = V(15), lo que nos conduce a dos opciones:
x1 = +
3,88 (aproximadamente), que corresponde con argumentos positivos en los logaritmos,
x2 = - 3,88 (aproximadamente), que corresponde con un argumento negativo para el logaritmos del denominador,
por lo que concluimos que la ecuación admite como única solución: x1 = +V(15) = +3,88 (aproximadamente).
3) Puedes aplicar las identidades trigonométricas:
(cosx)^2 = 1 / ( 1 + (tanx)^2 ), y (senx)^2 = (tanx)^2 / ( 1 + (tanx)^2 ).
También debes considerar que el intervalo corresponde al primer cuadrante, en el que tangente, coseno y seno toman valores positivos.
Espero haberte ayudado.
-
Camila Astrada
el 29/9/16Hola unicoos tengo dudas con este ejercicio:
Llegué a la respuesta de que a=1 y b=3, que estan bien, pero resolvi las derivadas laterales por LHopital, ¿está bien usar esa regla cuando no sabes si la funcion es derivable o no? No se me ocurre otra forma de resolver los limites
