-
Javi
el 29/9/16Buenas tardes, me podrian por favor ayudar con este problema de álgebra?
-Encuentra dos polinomios tales que al dividirlos aparezca q(x)=x2 -x -3 como polinomio cociente y r(x)= -3x2 -1 como resto.
Gracias de antemano :D
Gabriel
el 29/9/16Aquí tienes la ayuda. A ver si es útil.
Coge dos polimonios cualesquira, si quieres algo sencillo, del tipo (x-1) y (x+2).
En ese caso, para calcular el primer polinomio que te piden, calcula (x-1) · (x^2-x-3) + (-3x^2-1). El polinomio que te dé, es el que buscas.
Haces lo mismo con el otro polinomio.
Ahí lo tienes.
Antonio Silvio Palmitano
el 29/9/16Observa que estamos buscando dos polinomios A(x) y B(x) tal que, al hacer la división de A(x) por B(x) nos queda: cociente q(x) y como resto r(x). Luego, por el algoritmo de Euclides tenemos:
A(x) = B(x) * q(x) + r(x) (*), con grado de r(x), que es 2, menor que grado de B(x),
por lo que tenemos en el enunciado, el grado mínimo de B(x) debe ser 3. Luego, podemos elegir: B(x) = x^3, y a partir de la ecuación señalada (*) podemos calcular A(x).
Espero haberte ayudado.
-
Antonio Marin
el 29/9/16
Alguien me podria explicar como se descomponen las fuerzas en este ejercicio??? Sí, he visto el video de unicoos pero no consigo entender el por qué.
-
Manuel Ortiz
el 29/9/16Buenos días, ¿me podrían dar algunas ideas para resolver este problema? por favor.
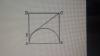
Una copa de papel de forma cónica con un diámetro superior de 8 cm y una profundidad de 6 cm esta lleno de agua. La copa pierde agua por abajo a razón de 2 centímetros cúbicos por minuto . ¿A que velocidad esta bajando el nivel del agua en el instante en el cual tiene exactamente 3 cm de profundidad?.
Antonio Silvio Palmitano
el 29/9/16La expresión del volumen para un semicono con altura h y radio de su base r es: V = (1/3)pi*h*r^2:
A medida que va perdiendo agua, la longitud de r y de h disminuyen, y en un instante t genérico, el volumen queda expresado como función de t:
V(t) = (1/3)pi * h(t) * ( r(t) )^2.
Luego, la relación entre altura y radio es constante: h(t) / r(t) = 6/8, despejamos y queda: r(t) = (4/3)*h(t),
luego sustituimos en la expresión del volumen y tenemos:
V(t) = (1/3)pi * h(t) * ( (4/3)*h(t) )^2, operamos y la expresión queda:
V(t) = (16/27)pi * ( h(t) )^3.
Luego, derivamos para encontrar la expresión del ritmo de pérdida de agua:
V ' (t) = (16/9)pi * ( h(t) )^2 * h ' (t).
Luego, a partir del enunciado tenemos: h(t) = 3, V ' (t) = - 2 (recuerda que el volumen de agua está disminuyendo), reemplazamos y nos queda la ecuación:
- 2 = (16/9)pi * ( 3 )^2 * h ' (t), resolvemos a la derecha y queda:
- 2 = 16pi * h ' (t), hacemos pasaje de factor como divisor, simplificamos a la izquierda y queda:
- 1 / (8pi) = h ' (t),
por lo que concluimos que la profundidad está disminuyendo a razón de 1/(8pi) cm/min.
Espero haberte ayudado.
-
Lucía
el 29/9/16 -
Facundo
el 29/9/16Dadas las matrices :
A = 1 2 B= 1 2 C= 0 12
-1 1 0 1 -2 -4
resuelve la ecuación A^2 X + BX = C, despejando el valor de la matriz incónita X
Antonio Silvio Palmitano
el 29/9/16Observa que en la ecuación matricial podemos extraer factor común por la derecha en el primer miembro y queda:
( A^2 + B )*X = C.
Luego, te queda calcular la matriz M = A^2 + B (lo haces y te queda invertible), y la ecuación queda:
M*X = C
luego multiplicas por la izquierda por la matriz inversa de M en ambos miembros y la ecuación queda:
M^(-1) * M * X= M^(-1) * C, observa que M^(-1) * M = I (matriz identidad de orden 2):
I * X = M^(-1) * C, resolvemos a la izquierda y llegamos a:
X = M^(-1) * C.
Luego debes hacer todos los cálculos.
Espero haberte ayudado.
César
el 29/9/16 -
Víctor Miranda
el 29/9/16 -
Víctor Miranda
el 29/9/16 -
Víctor Miranda
el 29/9/16Alternativamente vamos lanzando una moneda y un dado, el experimento termina cuando salga cruz o cuando obtengamos un cinco, empezamos lanzando la moneda ¿cuál es la probabilidad de acabar porque hemos obtenido un 5?
David
el 30/9/16La probabilidad de acabar a la primera, porque te salga cruz será 1/2
Si sale cara, la probabilidad de que acabemos pasa porque te salga un 5. La probabilidad sería (1/2)(1/6).
Pero puede ser que salga cara y un numero diferente a 5 y deberemos tirar la moneda otra vez. La probabilidad de ganar pasaría porque nos saliera una cruz.. en ese caso ganamos con una probabilidad de (1/2)(5/6)(1/2).. Pero... ¿y si sale cara? Deberemos tirar el dado. Ganaremos si sale un 5... LA probabilidad de ganar.. (1/2)(5/6)(1/2)(1/6)...
Si sale un numero diferente deberemos tirar la moneda otra vez. Ganaremos si sale cruz.. La probabilidad (1/2)(5/6)(1/2)(1/6)(1/2)..
Y así hasta el infinito.. La probabilidad será la suma de todas ellas... -
Víctor Miranda
el 29/9/16Halla todos los enteros positivos a y b, con b impar, tal que
1/a + 4/b=1/12
-
JRefusta
el 29/9/16Buenas! tenia algunas dudas sobre como hacer límites cuando tiende hacia infinito, sobretodo en este tipo de casos:
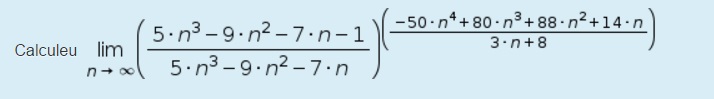
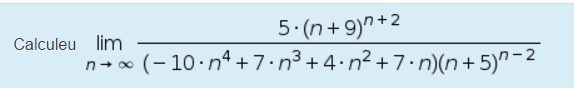
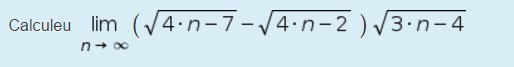
En los dos primeros ando muy perdido. En el tercero sé que primero debo resolver lo de dentro del paréntesis (con lo de a^2-b^2) pero una vez hecho no sé como seguir, agradecería vuestra ayuda!
