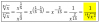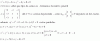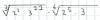Foro de preguntas y respuestas de Matemáticas

Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.

Ir a beUnicoos

Joship
el 27/9/16

hola , no he podido hacer este ejercicio, si alguien me ayuda por fa

••0 voto/s
•
Antonius Benedictus
el 28/9/16
Creo que es así, Jhossip:

•1 voto/s
•

Cancelar
Jose
el 27/9/16

Hallar h y k de modo que f resulte continua hice el lim de x tendiendo a 0 por derecha y me queda 0/0 lo que hice multiplicar por el conjugado arriba y abajo y me queda -x/ raiz de x por (4 raiz de x +16) y me trabe ayuda

••0 voto/s
•
Antonio Silvio Palmitano
el 27/9/16
Observa que puedes simplificar:
- x / ( V(x) * V(x + 16) ) = -1*x^1 / ( x^(1/2) * V(x + 16) ) = simplificamos potencias de x =
= - 1*x^(1 - 1/2) / V(x + 16) = -1*x^(1/2) / V(x + 16) = - V(x) / V(x + 16)
y al tomar el límite cuando x tiene a cero por la derecha queda: - 0/V(16) = - 0/4 = - 0 = 0.
Observa:
el numerador te quedó factorizado: N = -1*x
el denominador te quedó factorizado: D = V(x)*V(x + 16)
luego puedes simplificar los factores x (del numerador) con V(x) = x^(1/2) del denominador, que es lo que hemos hecho.
Espero haberte ayudado.

•0 voto/s
•
Antonius Benedictus
el 27/9/16
Te explicamos, José:

•1 voto/s
•

Cancelar
Matías
el 27/9/16
1. El e el máximo absoluto se da en x=4, pero a mí m da que no existe.. Me ayudan? El intervalo es en (2 + infinito )
••0 voto/s
•
Antonius Benedictus
el 27/9/16
No se lee bien, Matías.

•0 voto/s
•

Cancelar
Javier García
el 27/9/16

Como se simplifica esto? ⁵√x/³√x

••0 voto/s
•
Axel Morales Piñón.
el 27/9/16
Así Javier:

•1 voto/s
•
Desencadenado
el 27/9/16

•1 voto/s
•

Cancelar
The punk
el 27/9/16

Hola amigos tengo problemas para demostrar el apartado a) me podrían ayudar

••0 voto/s
•
Antonio Silvio Palmitano
el 27/9/16
Indicamos a los conjugados de z y u, respectivamente, como z' y u'.
|z - u|^2 = por propiedad = (z - u)(z' - u') = z*z' - z*u' - u*z' + u*u' =
Luego obsreva z*z' = |z|^2, u*u' = |u|^2 y (z*u')' = z'*(u')' = z'*u,
luego reemplazamos en el primero, el tercero y el cuarto término y seguimos la cadena de igualdades:
= |z|^2 - z*u' - (z*u')' + |u|^2 =
Extraemos factor común en los dos términos centrales:
= |z|^2 - ( z*u' + (z*u')' ) + |u|^2 =
Observa que en el agrupamiento tenemos la suma del complejo z*u' con su conjugado, por lo que tenemos:
= |z|^2 - 2*Re(z*u') + |u|^2.
Recuerda que la suma de un número complejo con su conjugado es igual al duplo de la parte real del número complejo.
Espero haberte ayudado.

•1 voto/s
•
Antonius Benedictus
el 27/9/16
Otra versión, punk:

•0 voto/s
•

Cancelar
Soyangel11
el 27/9/16

Como se factoriza una cónica degenerada??? Como esta por ejemplo:
x²+2xy-6x+y²-6y+8=0

Ayuda pls es urgente!!!Gracias de antemano

••0 voto/s
•
César
el 27/9/16
No creo que sea tema de secundaria, pero alla vamos.

•0 voto/s
•
Antonio Silvio Palmitano
el 28/9/16
Va otra forma, válida para tu ecuación:
Ordenamos términos, agrupamos y queda:
(x^2 + 2xy + y^2) - 6(x + y) + 8 = 0, factorizamos el primer agrupamiento:
(x + y)^2 - 6(x + y) + 8 = 0, hacemos la sustitución: w = x + y:
w^2 - 6w + 8 = 0, observa que es una ecuación polinómica cuadrática, aplicas la fórmula resolvente y sus raíces son: w1 = 2 y w2 = 4, factorizamos y queda:
(w - 2)(w - 4) = 0, luego sustituimos w por su expresión en función de x e y:
(x + y - 2)(x + y - 4) = 0.
Esta forma es aplicable solo en algunos ejercicios, como el tuyo, y la forma más general es la que te mostró el colega César.
Espero haberte ayudado.

•0 voto/s
•

Cancelar
Jose Luis
el 27/9/16

Averigua la relación que hay entre x e y sabiendo que se verifica:
ln y = 2x - ln 5

••1 voto/s
•
Antonius Benedictus
el 27/9/16
Es ésta, José Luis:

•0 voto/s
•

Cancelar
Franco
el 27/9/16

Buenas tardes, me podrian indicar los V o F con sus justificaciones, por favor

••0 voto/s
•
Antonius Benedictus
el 27/9/16
Te lo contamos, Franco:

•1 voto/s
•

Cancelar
Rafa
el 27/9/16

Sea B(P,r) el círculo del plano real con centro P y radio r>=0; es decir, B(P,r)={x∈R²tq d(P,x)≤r } Demostrar Si 0 ≤ s ≤ r - d(Q,P) entonces B(Q,s)⊆ B(P,r) mmmm un poco de ayuda pls

••0 voto/s
•
Antonius Benedictus
el 27/9/16
Te lo demostramos, Rafa:

•1 voto/s
•

Cancelar
Juan
el 27/9/16

Alguien me puede reducir esta operación paso por paso al máximo? La necesito para tomar ejemplo.

••0 voto/s
•
Desencadenado
el 27/9/16

•2 voto/s
•
Desencadenado
el 27/9/16
Operaciones con radicales 02- Extraer factores
•3 voto/s
•

Cancelar