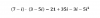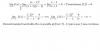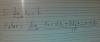-
Wayner
el 17/9/16Buenas Unicoos, necesita la ayuda.en estos ejercicios de funciones. La primera es una funcion compuesta y me dan como resultado: x^2-2x+5 y en la segunda: la opcion a) x (quiero saber el procedimiento para llegar alli). Muchas gracias.
Antonius Benedictus
el 17/9/16 -
Gaussiano
el 17/9/16 -
Angelo Villegas
el 17/9/16
Hola Unicoos, estoy un poco confuso con este ejercicio de Algebra Lineal (Geometria en el Plano y en el Espacio). Queria hacer incapie en como dar la ecuacion Normal a una recta, putno b) del ejercicio. Me podrian ayudar? Muchas Gracias -
Enrique Zapata
el 17/9/16Calcule el coeficiente que acompaña a x al desarrollar (3x + 2)3
3*3*3 = 27
2*2*2 = 8
x = 1
33 + 23 + 1 = 36
¿Esta bien hecha la manera en que lo hago?
Gracias por la ayuda.
Antonio Silvio Palmitano
el 17/9/16Recuerda el desarrollo de un binomio elevado al cubo, para una forma alternativa de resolución:
(a+b)^3 = a^3 + 3a^2*b + 3a*b^2 + b^3.
En tu ejercicio tienes: a = 3x, b = 2. Y como preguntan por el coeficiente del termino de grado 1, corresponde al tercer término del desarrollo:
3a*b^2 = 3(3x)*2^2 = 9x*4 = 36x, por lo que el coeficiente es 36.
Espero haberte ayudado.
Enrique Zapata
el 17/9/16
Antonio Silvio Palmitano
el 17/9/16Es el caso particular para este ejercicio. Observa que el enunciado pide el coeficiente del término con x (grado 1), y como en nuestro desarrollo tenemos:
a = 3x (expresión de grado 1), buscamos en el desarrollo el término con factor a (de grado 1), que resulta eser el tercer término.
En otros ejercicios puede haber variantes distintas a la de el que hemos discutido aquí.
Espero haberte ayudado.
-
Pablo Reyes
el 17/9/16Buenas tardes. les planteo la siguiente duda. Adjunto foto.
El límite me da cero, lo mismo que la imagen, entonces sería continua. Pero según los apuntes de mi profesor es una discontinuidad evitable, es decir, que la imagen de f(1) es = 0 y el Límite de la función cuando x-> 1 NO existe.
-
Alejandro Ocaña Martín
el 17/9/16hola buenas! como seria este ejercicio:
Sea π: ax +by+cz=1. Calcula los puntos invariantes cuando cambiamos el vector normal a n'=(a',b',c')
Antonio Silvio Palmitano
el 17/9/16Si los vectores n y n' son paralelos (n = kn', con k real distinto de 0), obtienes una ecuación del mismo plano, por lo que todos los puntos resultan invariantes.
Si los vectores n y n' no son paralelos, obtienes la ecuación de un nuevo plano que corta al anterior en una recta (L), por lo que planteamos:
Vector director de L: u = n x n' (producto vectorial de los vectores normales).
Luego, nos queda determinar un punto en común para los dos planos, por lo que planteamos el sistema de ecuaciones:
ax + by + cz = 1
a'x + b'y + c'z = 1
Luego, podemos ver que tenemos dos ecuaciones con tres incógnitas, por lo que podemos fijar el valor de una de ellas, por ejemplo: z = 0 (si no nos queda: a/a' = b/b', porque si ocurre ésto tendríamos que fijar el valor de otra de las incógnitas), y el sistema queda:
ax + by = 1
a'x + b'y = 1
Luego resuelves el sistema (por ejemplo con regla de Cramer) y obtendrás la solución: x = X, y = Y, donde las expresiones de X e Y quedan para que las calcules.
Luego, un punto de la recta que intersección entre los dos planos es: A(X,Y,0).
Luego, con el punto y el vector director conocidos, puedes plantear ecuaciones cartesianas (paramétricas o simétricas) de la recta L, que es el conjunto de puntos que está incluido en los dos planos.
Espero haberte ayudado.
-
Pedro
el 17/9/16 -
Carolina
el 17/9/16Hola Unicoos, estoy muy complicada con una integral me pueden ayudar por favor:
Muestre que:
la integral de 0 a infinito e^-x cos(x) = 1/2
gracias
Carolina
Antonio Silvio Palmitano
el 17/9/16Llamemos I a la integral original, a la que resolveremos por partes en dos pasos:
1°) u = cosx, de donde tenemos: du = -senx*dx, dv = e^(-x), de donde tenemos: v = -e^(-x), luego nos queda:
I = -e^(-x)*cosx - Integral( e^(-x)*senx*dx)
2°) para resolver la integral secundaria, planteamos:
u = senx, de donde tenemos: du = cosx*dx, dv = e^(-x), de donde tenemos: v = -e^(-x), luego nos queda:
I = -e^(-x)*cosx - ( -e^(-x)*senx + Integral(e^(-x)*cosx*dx )
Observa que en el segundo término del agrupamiento nos quedó la expresión de la integral original (I), distribuimos signos y nos queda:
I = -e^(-x)*cosx + e^(-x)*senx - I
hacemos pasaje de término y queda:
2*I = - e^(-x)*cosx + e^(-x)*senx
por último, multiplicamos por 1/2 en todos los términos, introducimos la constante de integración y llegamos a:
I = - (1/2)*e^(-x)*cosx + (1/2)*e^(-x)*senx + C.
Espero haberte ayudado.
-
Alex Barboza
el 17/9/16Hola disculpen podrían ayudarme con este problema, no se como hacerlo.
Un objeto se mueve de acuerdo a y= 31/2 sen(6πt - π/3) donde t se mide en minutos.
¿Cuantos ciclos se completa en 15 minutos y a que distancia hay desde el objeto hasta el origen cuando el t=0?
-
GabrielOrellana
el 17/9/16Saludos Unicoos, me podrian correguir el siguiente ejercicio, y en dado caso indicarme cual es la foma corecta de hacerlo. gracias de antemano
Antonio Silvio Palmitano
el 17/9/16Debes corregir en la anteúltima línea de tu desarrollo. Observa que vector genérico del subespacio Imagen (en este caso un polinomio del espacio vectorial P1) es:
2at + b = 2a*t + b*1, y observa que es combinación lineal de t y de 1, que son linealmente independientes, por lo que una base de la Imágen es: {t,1].
Espero haberte ayudado.
