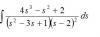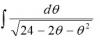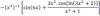Foro de preguntas y respuestas de Matemáticas

Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.

Ir a beUnicoos

Jordi Ramos
el 14/9/16

Hola amigos me ayudan con esta inecuacion no entiendo como resolverla, es el punto 1a

••0 voto/s
•
Desencadenado
el 14/9/16
asi Jordi

•0 voto/s
•

Cancelar
Anthony Zusaki
el 14/9/16

si se cumple : aba2b=99° hallar ¨b - a¨ ayuda porfavor

••0 voto/s
•
David
el 14/9/16
¿¿?? ¿aba2b??

•0 voto/s
•

Cancelar
Jean Martini
el 13/9/16

Hola, estoy estudiando para mi parcial de calculo, me mandaron unos ejercicios modelos y este no me sale.

••0 voto/s
•
Axel Morales Piñón.
el 14/9/16
Has intentado por fracciones parciales ¿¿??

•0 voto/s
•

Cancelar
Stefany
el 13/9/16

Buen día, necesito ayuda con el siguiente ejercicio

••0 voto/s
•
José Manuel
el 13/9/16
Esta integral ya fue preguntada una vez en el foro, aquí tienes, por cortesía del profesor Antonio.

•2 voto/s
•
Stefany
el 13/9/16
Gracias, la verdad es que soy nueva aquí

•0 voto/s
•

Cancelar
diego alexander
el 13/9/16

buenas tardes unicoos, tengo problemas con esta integral: ln²Xdx

••0 voto/s
•
Axel Morales Piñón.
el 14/9/16
Enunciado original Diego.... para ayudarte

•0 voto/s
•
Axel Morales Piñón.
el 14/9/16
Esperemos y sea esta Diego ...

•0 voto/s
•
Axel Morales Piñón.
el 14/9/16
Otro método ... el que te apetezca

•0 voto/s
•
diego alexander
el 14/9/16
muchas gracias hermanoo...!!!

•0 voto/s
•

Cancelar
Magalí
el 13/9/16

Hola a todos, mi profesor dice que está bien resuelta la derivada pero que puedo aprolijar aún más la respuesta. Me pueden ayudar a "aprolijar" la respuesta.

••0 voto/s
•
chado
el 13/9/16
fijate que podrias, bien esos terminos de exponente negativo, mandarlo al denominador, y luego sacarlo de factor comun, fijate que se repite en tu resultado 2 veces.
ademas en el segundo termino grande, el (-1) poder "eliminarlo" y cambiar el signo de toda la mitad
PD: perdon que no te lo escriba bien pero ahora no cuentos con celular ni acceso a un editor para poder hacertelo de manera prolija :( espero que me logres entender

•1 voto/s
•
chado
el 13/9/16

•1 voto/s
•
Desencadenado
el 13/9/16
Algo así Magalí

•1 voto/s
•

Cancelar
lizet
el 13/9/16

determinar el área sombreada de la figura limitada por x²+y²=25 y x=3

••0 voto/s
•
Antonio Silvio Palmitano
el 13/9/16
Observa que la circunferencia tiene al eje OX como uno de sus ejes de simetría, y que el eje OX divide a la región en dos mitades, por lo que plantearemos el área de la mitad "superior" y multiplicaremos por dos.
La mitad "superior" está limitada por "debajo" por el eje OX (cuya ecuación es y = 0), y por "arriba" por la semicircunferencia "superior", cuya ecuación explícita es: y = +V(25 - x^2), y que los valores del eje OX que comprende la región son los comprendidos entre 3 y 5.
Por lo tanto, el área de la región sombreada queda planteada:
A = 2 * Integral ( V(25 - x^2) )*dx, evaluada entre 3 y 5.
Recuerda que esta integral puede resolverse con la sustitución (cambio de variable): w = 5sent, como seguramente has visto en clase, o en los vídeos, a los que te recomiendo recurras.
Espero haberte ayudado.

•1 voto/s
•

Cancelar
Jordi García
el 13/9/16

Hola a todos, tengo una duda:
¿El apotema no tendría que medir x√3 en vez de (x√3)/2?
Gracias.

••0 voto/s
•
César
el 13/9/16
en un hexagono la ap=√r²-(l/2)²=√(x²-(x/2)²=x√3/2

•0 voto/s
•

Cancelar
Wayner
el 13/9/16
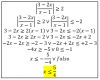
1. Buenas, una pregunta es las inecuaciones racionales, si tenemos un ejercicio cuando: x<b, al resolver el ejercicio (ya obtenidos los puntos critcos) y evaluar los intervalos desde -infinito al +infinitos, se van a tomar solo la(s) partes negativas? , me refiero por < y cuando x>b se tomarian solo donde los intervalos donde dio positivo o eso nada mas ocurre cuando hay 《》(mayor igual y menor igual).
••0 voto/s
•
David
el 14/9/16
Lo siento, no entiendo... Si nos envías el ejercicio concreto, el enunciado exacto y literal será más fácil ayudarte...

•1 voto/s
•

Cancelar
Augusto
el 13/9/16

Alguien que me explique porque mi profesor ha puesto que la derivada de y^2 es 2yy'. Supuestamente la explicación es la que está entre nubes pero no la entiendo...

••0 voto/s
•
Enrique Soler
el 13/9/16
En teoría la derivada de y^2 es 2y ya que al derivarlo la y quedaría elevada a 1.

De tal modo y^6 será 6y^5
Un saludo.

•0 voto/s
•
Antonio Silvio Palmitano
el 13/9/16
Debes tener en cuenta que en una ecuación del tipo: x^2 + y^2 = 1, tenemos definida implícitamente a y como una función cuya fórmula no conocemos, y si pudiésemos despejar nos quedaría:
y = g(x) (*), y su derivada quedaría: y ' = g ' (x) (**).
Por lo tanto, la ecuación implícita podríamos escribirla (observa que sustituimos y):
x^2 + ( g(x) )^2 = 1, hacemos pasaje de término y queda:
x^2 + ( g(x) )^2 - 1 = 0.
Observa que podríamos derivar término a término:
en el primero la derivada es directa (se trata de una potencia, por lo que baja el exponente como factor, y queda el exponente disminuido en uno),
en el segundo término tenemos una composición de funciones (tenemos un cuadrado cuyo argumento es una función), por lo que debemos aplicar la regla de la cadena,
en el tercer término tenemos que es constante y su derivada es cero,
luego derivamos y queda:
2x + 2g(x)*g ' (x) = 0.
Luego, como hemos señalado en las ecuaciones (*) y (**), reemplazamos y nos queda:
2x + 2y*y ' = 0.
Espero haberte ayudado.

•1 voto/s
•

Cancelar