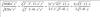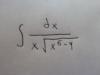-
hola!! Me podrían ayudar con estos dos límites de la forma (0/0)..
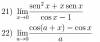 al rato son muy sencillas, pero me quedo pegada al resolverlas.. :cc Graaciaas!!
al rato son muy sencillas, pero me quedo pegada al resolverlas.. :cc Graaciaas!!

Antonio Silvio Palmitano
el 12/9/1621)
Puedes comenzar por extraer factor común en el numerador, y multiplicar en el numerador y en el denominador por (1+cosx), aplicas distribuyes y aplicas identidad trigonométrica en el denominador, lo haces y la expresión de la función queda:
senx*(senx + x) / ( - (senx)^2 ) = simplificamos, resolvemos signos y queda:
= - (senx + x)/senx = distribuimos, simplificamos en el primer término y queda:
= -1 - x/senx. Luego pasas al límite, y observa que para el segundo término tienes que es igual a 1 (es un límite trascendente que has visto en clase con seguridad), por lo que el límite es igual a -2.
22)
Puedes aplicar la identidad trigonométrica de la diferencia entre dos cosenos: cosu - cosv = -2*sen((u+v)/2)*sen((u-v)/2), observa que para este ejercicio tienes: u = a+x, v = x, reemplazamos y el numerador de la expresión de la función queda:
-2*sen((a+x+a)/2)*sen((a+x-x)/2) = -2*sen((2x+a)/2)*sen(a/2).
Luego, la expresión de la función al dividir al numerador y al denominador por 2 queda:
- sen((2x+a)/2)*sen(a/2) / (a/2).
Luego, como tienes un producto, puedes tomar limite para cada factor por separado y queda:
L = - sen(2x/2)*1 = - senx.
Observa que el límite del primer factor es directo, y observa que para resolver el límite del segundo factor, podemos plantear la sustitución (cambio de variable): w = a/2, y el límite queda igual a 1, por límite trascendente como en el ejercicio anterior.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 12/9/16j)
Debemos plantear dos ecuaciones: una de cantidades de solución y otra de cantidades de ácido puro. Llamemos:
x: cantidad de ácido al 30%, y: cantidad de ácido al 50%, por lo que tenemos:
x + y = 10 (cantidad total de solución buscada)
0,3x + 0,5y = 0,42*10 (cantidad total de ácido puro).
k)
Llamemos. x. cantidad de rosas en total, y: cantidad de tulipanes en total, z: cantidad de lilas en total, para armar cinco bouquetes. Tenemos el sistema:
x + y + z = 120 (cantidad de flores necessarias)
6x + 4y + 3z = 610 (costo total)
x = 2(y + z) (cantidad de rosas en relación a las cantidades de tulipanes y lilas).
l) Llamemos a las distancias recorridas: x: por el auto, y: por el camión, z. por el bus. Tenemos el sistema:
x + y + z = 85 (distancia total recorrida entre los tres vehículos)
1,1x + 1,5y + 0,4z = 73,5 (cantidad total emitida de dióxido de carbono)
1,5x + 0,2y + 1,8z = 149,5 (cantidad total emitida de NO).
Queda para que resuelvas los sistemas de ecuaciones.
Espero haberte ayudado.


Ulises Torres
el 12/9/16gracias, muchas gracias, solo una duda, en la última ecuacion del ejercicio k)
dice que quiere tener el doble de rosas que las otras dos flores en cada ramo.
y me indico que la ecuacion queda x=2(y+z)
no queda mas bien asi?: 2x-y-2=0
es que me quedo esa duda y la verdad no me queda muy claro
de antemano gracias!!

Antonio Silvio Palmitano
el 12/9/16Observa la consigna para la tercera ecuación: "el doble de rosas que las otras dos flores en cada ramo".
Entendemos que la cantidad de rosas (x) debe ser el doble (2*) de la cantidad de flores de las otras dos clases juntas (y + z), y de ahí tenemos la ecuación: x = 2*(y + z).
Observa también que la cantidad de rosas (x) es el mayor número entre los tres.
En la ecuación que propones: 2x - y - z = 0, despejas x y queda:
x = (y + z)/2
a la que le correspondería la consigna: "la cantidad de rosas (x) es la mitad (/2) de la cantidad de flores de las otras dos clases juntas (y + z)".
La "traducción" de nuestro lenguaje coloquial al lenguaje algebraico ("de las ecuaciones") es un ejercicio que debemos hacer todos, ya que las palabras (en cualquier idioma) pueden llevar a ecuaciones incorrectas si hacemos las cosas con apuro. Es muy común, a todos nos ocurre, que debamos ser cuidadosos en los planteos de esta clase de problemas.
Espero haberte ayudado.
-
Buenas noches,
Tras muchos años sin dar matemáticas me he metido en la carrera de ADE, y en primero tengo la asignatura de Matemáticas I, la cual según la profesora es un recuerdo de todo lo dado en la ESO y Bachillerato. ¿El problema? Que no recuerdo prácticamente nada. Gracias a vosotros he podido sacar los ejercicios del tema 1 que estamos dando de máximos, ínfimos, mínimos, las sucesiones, los dominios, etc... Pero me da mucha vergüenza admitir que el primer ejercicio, este tan sencillo, no soy capaz de realizarlo. He visto vídeos de representar conjuntos más facilitos y entiendo como se sitúan en la recta real, pero los subconjuntos de este tipo me tienen bloqueado... Hay algún video al respecto? podríais ayudarme aunque sea realizando dos, los que creáis mas difíciles y así veo como se hacen?
Perdonad mi absoluta ignorancia y siento si es demasiado fácil. Gracias de antemano.


David
el 12/9/16c,d y e son inecuaciones, algunas de ellas con valor absoluto... Te sugiero veas TODOS los vídeos de esas lecciones Inecuaciones
El a) simplemente es el intervalo de todos los numeros comprendidos entre el -8 y el 2 (este ultimo incluido), además de los puntos x=-12 y x=-8,9... De nuevo te sugiero los vídeos de inecuaciones para que veas como representar intervalos...
Nos cuentas despues ¿ok?...Se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas, sobre todo si son universitarias y debemos hacer una excepción) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. #nosvemosenclase Nos cuentas ¿ok?
-
Alguien me ayuda con este ejercicio.
Ubicaria que el complejo esta en el 4 cuadrante..... peor no logro entender y sacar la primera parte donde z^6= -8i


Antonio Silvio Palmitano
el 12/9/16Observa que el número complejo -8i está representado por el punto de coordenadas (0,-8) en el eje OY, por lo que su módulo es 8, y su argumento es 270° = 3pi/2, tal como se puede visualizar con un gráfico. Luego, tenemos la ecuación.
z^6 =(8)(270°), luego despejamos (expresamos raíz sexta de 8 como (6V)(8))y queda:
z = (6V)( (8)(270°) ), luego aplicamos la fórmula de De Moivre para las raíces y queda:
z = ( (6V)(8) )( (270° + 360° * k) / 6 ), con k = 0, 1, 2, 3, 4, 5.
Luego, observa que podemos trabajar en la expresión del módulo: (6V)(8) = (6V)( 2^3 ) = V(2), y que podemos distribuir el denominador y resolver en la expresión general del argumento y queda: 270°/6 + 360° * k / 6 = 45° + 60° * k.
Luego, todas las soluciones tendrán módulo V(2) y sus argumentos serán (evaluamos para los seis valores de k, en indicamos a los argumentos como Ai):
Ao = 45°, A1 = 105°, A2 = 165°, A3 = 225°, A4 = 285°, A6 = 345°.
Y como bien has señalado, nos piden las soluciones que pertenecen al cuarto cuadrante, por lo que tenemos que las soluciones son (las expresamos en forma polar y en forma trigonométrica, con los argumentos expresados en grados):
z5 = (V(2))(285°) = V(2)*(cos285° + i*sen285°)
z6 = (V(2))(346°) = V(2)*(cos345° + i*sen345°).
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 12/9/16Puedes multiplicar al numerador y al denominador por x^5, y la expresión de la función que debes integrar queda:
f(x) = x^5 / ( x^6 * V(x^6 - 4) ).
Luego, plantea la sustitución (o cambio de variable):
w^2 = x^6 - 4, de donde tienes:
w^2 + 4 = x^6, y también tienes:
2w*dw = 6x^5 * dx, de donde haces pasaje de factor como divisor, despejas y queda: (1/3)*w*dw = x^5 * dx.
Luego sustituimos y la integral queda:
I = (1/3) * Integral( 1/(w^2 + 4) )*dw
Luego planteamos una nueva sustitución:
w = 2t, de la que tenemos: dw = 2dt, y también tenemos: w^2 + 4 = 4t^2 + 4 = 4*(t^2 + 1), sustituimos, extraemos factores constantes, simplificamos y queda:
I = (1/6)*Integral( 1 / (t^2 + 1) )*dt = (1/6)*arctan(t) + C = (1/6)*arctan(w/2) + C,
y solo queda sustituir w = V(x^6 - 4).
Espero haberte ayudado.
-
Buenas unicoos, alguno podrá ayudarme a resolver este sistema de ecuaciones? no logro hacerlo de ninguna manera y ya he probado varios caminos. Lo agradecería mucho.


Antonio Silvio Palmitano
el 12/9/16Puedes dividir miembro a miembro entre las dos primeras ecuaciones (observa que los denominadores deben ser distintos de cero para que tenga sentido la tercera ecuación), simplificas y queda:
x/y = (x - 3,2)/(y - 4,1), luego haces pasajes de divisores como factores y queda:
x(y - 4,1) = y(x - 3,2), luego distribuyes y queda.
xy - 4,1x = xy - 3,2y, luego haces pasaje de término, cancelas y queda:
-4,1x = -3,2y, luego haces pasaje de factor como divisor, resuelves y queda:
x = (32/41)y.
Luego puedes sustituir en la tercera ecuación para buscar a los valores de y, y continuar tu trabajo.
Espero haberte ayudado.