-
Buenas, no entiendo como pasa de la parte subrayada a la de los corchetes, a ver si alguien puede aclararmelo, gracias de antemano.
-
Hola,
me podrían ayudar con esta edo por favor?
es muy difícil y no me da el supuesto resultado adjunto, no se si estará mal.
Alguien conoce alguna calculadora online de Ec. diferenciales?
Gracias -
Buenas unicoos.
tengo casi resuelto este ejercicio de ecuacion, pero no se terminarlo pues he llegado a la solucion general implicita y suponngo que tengo que llegar a la sol. general Explicita, como seria?
Esta toda bien resuelta? ?
gracias -
Para dividir |cos x| / cos x, si seria un uno en valor aboluto como resultado, o de plano no se puede dividir. saludos


Antonio Silvio Palmitano
el 28/8/16Debes tener en cuenta la definición de valor absoluto:
si u > 0, tienes |u|/u = u/u = 1
si u < 0, tienes |u|u -u/u = -1
observa que u debe ser distinto de cero.
Observa que en tu ejercicio, tienes u = cosx:
si cosx > 0 ( intervalo (-pi/2, pi/2)) tienes: |cosx|/cosx = 1,
si cosx < 0 (intervalo (-pi, pi/2) u (pi/2,pi)) tienes: |cosx|/cosx = -1.
Espero haberte ayudado. -
Quisiera que me aclaren mis dudas acerca de este problema:
Me piden hallar la ecuaciones de la recta que pertenece a la familia de rectas α(x+2y-5)+β(3x-2y-1)=0 y que
a. Sea paralela al eje OX
b. Sea paralela al eje OY


Antonio Silvio Palmitano
el 28/8/16Recuerda que las rectas paralelas al eje de abscisas OX tienen ecuaciones con la foma y = k, con k perteneciente al conjunto de los números reales. Observa que la ecuación no contiene términos con x, por lo que deben anularse estos términos en la ecuación de la familia de rectas.
Análogamente, recuerda que las rectas paralelas al eje de ordenadas OY tienen ecuaciones con la forma x = k, con k perteneciente al conjunto de los números reales. Observa que estas ecuaciones no contien términos con y, por lo que deben anularse estos términos en la ecuación de la familia de rectas.
α(x+2y-5)+β(3x-2y-1)=0t
distribuimos y queda:
αx + 2αy - 5α + 3βx - 2βy - β = 0
agrupamos términos según x e y, y queda:
(αx + 3βx) + (2αy - 2βy) + (- 5α- β) = 0
luego extraemos factor común en los agrupamientos y queda:
(α + 3β)x + (2α - 2β)y + (- 5α- β) = 0 (*)
a) Rectas paralelas a OX, planteamos:
α + 3β = 0, que al despejar nos conduce a:
α = - 3β
luego sustituimos en la ecuación señalada (*), operamos y queda:
-8βy +14β = 0
extraemos factor común a la izquierda y queda:
β(-8y + 14) =0
hacemos pasaje de factor como divisor y queda:
-8y + 14 = 0
por último, despejamos y, simplificamos y queda:
y = 7/4.
b) Rectas paralelas a OY, planteamos:
2α - 2β = 0
despejamos y llegamos a:
α = β
luego sustituimos en la ecuación señalada (*), operamos y queda:
4βx - 6β = 0
extraemos factor común a la izquierda y queda:
β(4x - 6) = 0
hacemos pasaje de factor como divisor y queda:
4x - 6 = 0
por último despejamos, simplificamos y llegamos a:
x = 3/2.
Espero haberte ayudado. -
Hola me ayudan no se me ocurre como resolverlo.
No entiendo como hacer el conteo.
Para verlo mas grafinente me arme las distintas combinaciones con 4 numeros y conte donde aparece el 1 y me da 28.
Gracias

Antonio Silvio Palmitano
el 28/8/16Observa que al tirar cuatro dados, pueden salir cuatro de un total de seis números (1,2,3,4,5,6), y pueden repetirse, por lo tanto la cantidad total de resultados posibles es: |T| = 6^4 = 1296.
Luego, hacemos una partición:
a) No sale ningún 6: pueden salir cuatro de un total de cinco números (1,2,3,4,5), y pueden repetirse, por lo tanto la cantidad de resultados posibles es: |A| = 5^4 = 625.
b) Sale al menos un seis (observa que son los que faltan en el caso anterior), por lo tanto la cantidad de casos posibles es: |B| = 1296 - 625 = 671.
Luego, la proporciones para cada uno de los dos casos serán:
Pa = |A| / |T| = 625/1296
Pb = |B| / |T| = 671/1296
observa que la segunda es mayor que la primera, por lo que concluimos que el esposo del Sr Galíndez lavará los platos más veces en promedio.
Espero haberte ayudado.
-
hola, me pueden ayudar con este ejercicio de numeros complejos, necesito encontrar el valor de z perteneciente a los complejos que verifique la ecuacion, gracias
Usuario eliminado
el 28/8/16Hola Joaquin. No es un solo punto.. Es un lugar geometrico. Particularmente es 8x^2+9y^2+32x=40
Trabajemos un poco esa expresión. Consideremos z=x+iy=(x,y)
|z+3|=|(x,y)+(3,0)|=|(3+x,y)|=sqrt((3+x)^2+y^2)
|z+1|=|(x,y)+(1,0)|=|(x+1,y)|=sqrt((x+1)^2+y^2)
Para finalizar tienes
sqrt((x+3)^2+y^2)+sqrt((x+1)^2+y^2)=6
Elevando un par de veces al cuadrado y haciendo trabajo algebraico llegas a la elipse de arriba. Espero que te sirva. Saludos.







_Thumb.jpg)

_Thumb.jpg)


_Thumb.jpg)









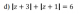

_Thumb.jpg)

_Thumb.jpg)

_Thumb.jpg)

_Thumb.jpg)
