-
Buenas tardes.¿Me pueden ayudar con este ejercicio?
Tengo 20 metros de tela metálica para construir un corral rectangular que quiero hacer pegado a la pared trasera de mi cortijo. ¿De qué forma puedo hacerlo para tener el área más grande posible? -
Usuario eliminado
el 27/8/16Para la primera tienes que, como primer paso, aplicar derivada de cociente. Esto queda [(x^2*e^x)'*(x+1)-(x+1)'(x^2*e^x)]/(x+1)^2. Para el primer sumando del dividendo debes aplicar la derivada de un producto. Esto es [[(x^2)'*(e^x)+(x^2)*(e^x)]*(x+1)-(x+1)'(x^2*e^x)]/(x+1)^2=[[2xe^x+x^2*(e^x)]*(x+1)-(x+1)'(x^2*e^x)]/(x+1)^2. Para el segundo sumando queda [[2xe^x+x^2*e^x]*(x+1)-x^2*e^x]/(x+1)^2. Los trabajos de simplificación te los dejo.
Para la segunda derivada tenes que aplicar la regla de la cadena varias veces. 2*cos(sqrt(x+1))*[cos(sqrt(x+1))]'=2*cos(sqrt(x+1))*[sin(sqrt(x+1))*[sqrt(x+1)]']=2*cos(sqrt(x+1))*[sin(sqrt(x+1))*[1/(2*sqrt(x+1))*(x+1)']]=2*cos(sqrt(x+1))*[sin(sqrt(x+1))*[1/(2*sqrt(x+1))]]
Espero que te sirva. Saludos. -
Hola a todos, vuelvo a poner el mismo ejercicio que nadie me ha sabido contestar (imagen adjunta).
Para calcularlo hay que saber que un sistema es incompatible si y solo si existe un número real t tal que: (a1,b1) = t · (a2,b2) pero c1 no= t · c2.
Gracias.


Antonio Silvio Palmitano
el 30/8/16En el primer sistema, planteamos:
Despejamos y en la primera ecuación y queda: y = 1/2 - (3/2)x.
Luego, sustituimos en la segunda ecuación y queda: bx + (a +1)(1/2 - (3/2)x ) = 3, distribuimos manteniendo el primer agrupamiento en el segundo término de la izquierda y queda:
bx + (a + 1)/2 - (3/2)(a + 1)x = 3, hacemos pasaje de término buscando agrupar términos semejantes y queda:
bx - (3/2)(a + 1)x = 3 - (a + 1)/2, extraemos factor común a la izquierda, denominador común a la derecha, resolvemos y queda:
(b - (3/2)a - 3/2)x = (5 - a)/2.
Luego, para que tengamos incompatibilidad, debemos tener una identidad (igualdad sin incógnita) absurda, por lo tanto planteamos
b - (3/2)a - 3/2 = 0, que al despejar y operar queda: b = (3/2)(a + 1)
(5 - a)/2 distinto de 0, que al despejar nos queda: 5 distinto de a.
En el segundo sistema, planteamos:
Despejamos x en la primera ecuación y queda:
x = 1 - by (*), sustituimos en la segunda ecuación y queda:
3(1 - by) + ay = 3, distribuimos a la izquierda y queda:
3 - 3by + ay = 3, hacemos pasaje de término, buscando agrupar términos semejantes y queda:
-3by + ay = 3 - 3, extraemos factor común a la izquierda, resolvemos a la derecha y queda
(- 3b + a )y = 0.
A continuación observa que tenemos dos opciones:
1)
Si -3b + a = 0, de la que al hacer pasaje de término nos queda: a = 3b, reemplazas y queda:
( -3b + 3b)y = 0, luego:
0y = 0, resolvemos a la izquierda y llegamos a la igualdad:
0 = 0, que es una identidad verdadera, por lo que concluimos que el sistema es compatible indeterminado en este caso.
2)
Si -3b + a es distinto de 0, de la que al hacer pasaje de término nos queda: a distinto de 3b, podemos hacer pasaje de factor como divisor y la ecuación queda:
y = 0/(-3b + a) resolvemos (observa que el denominador no es nulo para esta opción) y queda
y = 0,
luego reemplazamos en la ecuación señalada (*) y queda:
x = 1 - b*0, resolvemos y queda
x = 1, por lo que el sistema resulta compatible determinado para esta opción, y su solución es x = 1, y = 0.
Observa además que este sistema nunca es incompatible.
Espero haberte ayudado. -
hola unicoos¡
me he quedado a medias con esta ecuacion . me he parado en la integral de la funcion P con respecto a dx...
como continuaria el ejercicio?
muchas gracias -
hola,la funcion cuadratica y = 2x² -4x + 2 ami me sale asi Xν= -(-4 ⁄ 2×2=4 ⁄ 4=1 Yν=1x²-4x .1+2=1-4x+2=-1 y luego es los puntos de cortes y la ecuacion de segundo grado pero los puntos de cortes siempre es x=0 tengo esta duda y seria y=-1? y la ecuacion de segundo grado es 1x²-4x+2?? porfavor alguien me ayuda con esto
-
hola,alguien me ayuda con esto : dibuja la recta de ecuacion y = 3x - 1 dando las cordenadas de sus tres de sus puntos y ¿cual es la pendiente? ¿y la ordenada en el origen? ¿crece o decrece? . la pendiente yo creo que es 3x y la ordenada en el origen es -1 pero no se como dibujarla
-
no me sale, 5^x+1 + 5^x +5^x+1 = 81 / 5
-
Hola unicoos ,me ayudan con este problema no tengo idea como resolverlo ,alguien q me explique por favor.
-
hola gente, alguien que me ayude con este ejercicio? gracias
tambien quisiera que me aclarasen si en este tipo de ejercicios hay que pasarlo todo a la misma unidad o no importa , es decir, los centimetros cuadrados a centimetros, y viceversa







_Thumb.jpg)


_Thumb.jpg)
_Thumb.png)

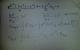



_Thumb.png)

_Thumb.png)

_Thumb.png)

_Thumb.png)

_Thumb.png)






_Thumb.jpeg)

_Thumb.jpg)
