-
Encuentre la ecuación para el plano tangente y la recta normal a la superficie
x^2 + y^2 - 2xy - x+3 - 6√z= -4
En el punto Po = (2, -3, 9 )
Po= p sub cero, no pude escribirlo bien en la pagina, espero me entiendan amigos!! Ayudenme por favor!!
-


Jose Ramos
el 25/1/20La distancia viene dada en la unidad arbitraria que se tome para el sistema de referencia en el que se trabaja. En tu caso estás trabajando en un sistema de referencia ortonormal formado por un punto O=(0,0,0) origen y tres vectores i, j, k perpendiculares entre sí y módulo 1. La unidad de distancia es el módulo de dichos vectores.
-
Determine una aproximación cubica f(x,y)= Ln2(3x-5y+1) alrededor del punto x0 , y0 = (1, -1)


Breaking Vlad
el 27/1/20se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)
-
Estudie la continuidad de la función f(x.y)= x2y2⁄ (x2y2+(x2- y2)2)
(x,y)≠(0,0)
(x,y)=(0,0) en todos los puntos de su dominio.


Breaking Vlad
el 27/1/20se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)
-


Antonio Silvio Palmitano
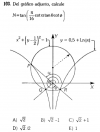
el 25/1/20Planteas la ecuación cartesiana explícita de la recta que pasa por los puntos A(-a,0) y B(0,a) que tienes indicados en tu figura, y queda:
y = x + a;
luego, planteas la ecuación cartesiana de la recta paralela al eje OX que pasa por el vértice superior del triángulo oblicuo que tienes sombreado en tu figura, y queda:
y = b;
luego, planteas la intersección entre las dos rectas cuyas ecuaciones hemos determinado, y tienes que se cortan en el punto: C(b-a,b),
cuya proyección sobre el eje OX determina el punto: D(b-a,0)
Luego, tienes que los vértices del triángulo sombreado son los puntos: O(0,0), A(-a,0) y C(b-a,b).
Luego, planteas la expresión del triángulo rectángulo ADC (observa que el triángulo oblicuo sombreado está incluido en él), y queda:
AADC = (1/2)*|AD|*|DC| = (1/2)*b*b = (1/2)*b2 (1).
Luego, planteas la expresión del triángulo rectángulo ODC (observa que el triángulo oblicuo sombreado no está incluido en él), y queda:
AODC = (1/2)*|OD|*|DC| = (1/2)*(b - a)*b = (1/2)*b*(b -a) (2).
Luego, observa que los dos triángulos cuyas áreas hemos expresado y el triángulo oblicuo sombreado AOB cumplen la relación:
AOC ∪ ODC = ADC,
luego, y teniendo en cuanta que los triángulos AOC y ODC solo comparten el lado común OC, planteas la relación entre sus áreas, y queda:
AAOC + AODC = AADC,
sustituyes las expresiones señaladas (1) (2), y queda:
AAOC + (1/2)*b*(b - a) = (1/2)*b2,
restas (1/2)*b*(b - a) en ambos miembros, y queda:
AAOC = (1/2)*b2 - (1/2)*b*(b - a),
extraes factores comunes, y queda:
AAOC = (1/2)*b*[b - (b - a)],
resuelves el último factor, y queda:
AAOC = (1/2)*b*a (3).
Luego, tienes el valor del área del triángulo oblicuo sombreado:
AAOC = 8 (en u2), sustituyes la expresión señalada (3) en el primer miembro, y queda:
(1/2)*b*a = 8, multiplicas por 2 en ambos miembros (observa que este valor es positivo y distinto de cero), y queda:
b*a = 16 (4) (en u),
y aquí observa que los posibles pares de valores enteros positivos (a,b) son: 1
(1,16) (4a),
(2,8) (4b),
(4,4) (4c),
(8,2) (4,d),
(16,1) (4,e).
Luego, planteas la expresión de la tangente del ángulo de inclinación (φ) del segmento OC con respecto al semieje OX positivo (observa que esta expresión corresponde a la pendiente de dicho segmento), y queda:
tanφ = |DC|/|OD|, sustituyes las expresiones de las longitudes de los segmentos, y queda:
tanφ = b/(b - a) (5).
Luego, planteas la expresión de la medida del ángulo θ que tienes señalado en tu figura (observa que este ángulo es obtuso, por lo que pertenece al segundo cuadrante) en función del ángulo φ, y queda:
θ = φ + 90°,
aplicas la identidad trigonométrica del la tangente de los ángulos cuyas medidas difieren en 90°, y queda:
tanθ = -cotgφ,
expresas a la tangente del ángulo θ en función de su cotangente, expresas a la tangente del ángulo φ en función de su cotangente, y queda:
1/cotgθ = -1/tanφ,
y de aquí despejas:
cotgθ = -tanφ,
sustituyes la expresión señalada (5) en el segundo miembro, y queda:
cotgθ = -b/(b - a) (6).
Luego, evalúas la expresión señalada (6) para los pares ordenados (a,b) señalados (4a) (4b) (4c) (4d) y (4e), y tienes:
cotgθ = -16/(16 - 1) = -16/15 ≅ -1,067 para el par (1,16),
cotgθ = -8/(8 - 2) = -4/3 ≅ -1,333 para el par (2,8),
cotgθ no está definida para el par (4,4),
cotgθ = -2/(2 - 8) = 1/3 ≅ 1,333 para el par (8,2), que no tiene sentido para este problema (recuerda que el ángulo θ pertenece al segundo cuadrante),
cotgθ = -1/(1 - 16) = 1/15 ≅ 0,067 para el par (2,8), que no tiene sentido para este problema (recuerda que el ángulo θ pertenece al segundo cuadrante);
luego, puedes concluir que la cotangente del ángulo señalado θ toma el valor -16/15, para los números enteros positivos: a = 1 y b = 16, y que el valor mencionado es el máximo para pares de valores enteros positivos.
Espero haberte ayudado.
-


Breaking Vlad
el 27/1/20se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)
-


Breaking Vlad
el 27/1/20se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)