-
hola me podrian ayudar con este ejercicio?, no tengo idea de como empezar, necesitaria que me ayuden a razonarlo, no me importa resolverlo sino entenderlo... Gracias!
-
Hola amigos de UNICOOS; les escribo nuevamente para que me ayuden con este problema de cambio de base. Lo mando en archivo adjunto. Espero su respuesta. Muchas gracias.
Saludos desde Curico Chile
Boris

BORIS MUÑOZ REYES
el 4/7/16HOLAAA!! GRACIAS POR TU RESPUESTA PERO EN LA UNIVERSIDAD ME ENTREGARON OTRA SOLUCION; POR ESO QUEDE CON LA DUDA. SI FUERA AL REVÉS NO ME QUEDA CLARO COMO OBTIENEN LOS VECTORES V1, V2 Y V3. ME PUEDES DAR LA SOLUCION SI ES AL REVÉS POR FAVOR. TE ENVIO EN ARCHIVO ADJUNTO LA SOLUCION QE ME ENTREGARON. DE ANTEMANO GRACIAS.
SALUDOS
BORIS -
Si me piden la ecuacion d euna elipse de centro(-3;2) y que es tg a los ejes coordenados, sabiendo tambien sus ejes de simetria son paralelos a los ejes x e y. Como deberia encararlo?
Lo unico que se me ocurre, es marcar el centro en un sistema de ejes. Y como la elipse es tg a los ejes, entonces podria deducir que a=2, que es la distancia desde el centro al punto de tangencia. Pero nose la verdad como es la manera correcta. Gracias de antemano

Antonio Silvio Palmitano
el 4/7/16Primero haz un gráfico para visualizar mejor la situación, y verás:
la elipse está ubicada en el segundo cuadrante (x<0 e y>0),
el semieje mayor es paralelo a x, y su longitud está determinada por la distancia entre los puntos C(-3,2) y A(0,2), por lo que su longitud es a = 3,
el semieje menor es paralelo a y, y su longitud está determinada por la distancia entre los puntos C(-3,2) y B(-3,0), por lo que su longitud es b = 2,
por lo tanto, la ecuación canónica de la elipse es:
((x + 3)^2) / 9 + ((y - 2)^2) / 4 = 1,
y luego con la relación entre semiejes puedes calcular la semidistancia focal: c = V(a^2 - b^2) = V(5),
y a partir de aquí, ya puedes indicar vértices y focos (observa que un vértice se encuentra en el eye y, y otro se encuentra en el eje x.
Espero haberte ayudado. -

Thomas Nuñez
el 3/7/16No estoy seguro, Pero creo que puedes elevar el numerador y el denominador a la n y asi te quedara: el numerador sin toda la raiz y el denominador n^n.
n^n es igual a nxn...nxn (n por n, n cantidad de veces) que es parecido a lo que hay en el numerador.
entonces te queda nx(n+1)x......(n+n) que seria igual a (n^n)xn! (n! por que multiplicas por 1,2,3,4...(n-1),n y (n^n) por que multiplicas por n, n cantidad de veces) Espero que hayas entendido.
El limite es igual a n! o infinito (no se como hacer el simbolo de infinito :( )
ATENCION: Esto esta mal ya que no se puede elevar el numerador y denominador a la n como dije al principio, la respuesta de Antonio tiene mas sentido





_Thumb.jpg)



_Thumb.jpg)

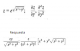


_Thumb.jpg)



_Thumb.png)

_Thumb.jpg)





_Thumb.jpeg)






_Thumb.jpg)

_Thumb.jpg)


