-


David
el 14/4/16Si 4=2.(1+R)^20, pasa el 2 dividiendo al otro miembro... 2=(1+R)^20... Haz la raiz veinteava en ambos miembros... 2^(1/20) = 1+R.... R=2^(1/20)-1...
En el segundo, a 1,07^t llamale z..... Te quedará 4200.(z-1)=2065.z... 4200.(z-1)=2065.z... 4200z-4200=2065z... 2135z= 4200... z=1.967
Por tanto 1,967=1,07^t... Eso es una ecuacion exponencial que se hace aplicando logaritmos... Ecuaciones exponenciales y logaritmicas
Haciendo logaritmos en ambos miembros de la expresion... log 1,967 = log 1,07^t... log 1,967 =t. log 1,07... t= log 1,967 / log 1,07 =0,294 / 0.0294 = 10 años
-
hola alguien me podría ayudar con este ejercicio, gracias.
Sea la función polinómica g(x) = 3x^2 - 18x + 4a , halla el valor de a sabiendo que g(x) es divisible entre (x -2). Con el valor de a hallado, encuentra las raíces y escribe su descomposición factorial. -
Hola, alguien me podría decir como encarar el enunciado A y B, entiendo que para que sea un conjunto generador B={(1,1),(2,0),(-1,1)}, lo igualo a (x,y) = a.(1,1) + b(2,0) + c(-1,1) siendo 'k' escalares, al resolver me queda un sistema de 2 ecuaciones con 3 incognitas, las primera ecuacion me queda 'x= c + 2m -c' y la segunda 'y= a + c' como puedo resolver ese sistema de ecuaciones y que me quede un sistema generador?


David
el 14/4/16Para que sea un conjunto de generadores, dado que estás trabajando en dos dimensiones (R²) bastará con que el rango de la matriz B sea 2...
Simplemente... Echale un vistazo... RANGO de una matriz por determinantes 01
Por otro lado, tal y como lo estabas planteando las ecuaciones resultantes de (x,y) = a.(1,1) + b(2,0) + c(-1,1) son x=a+2b-c....... y=a+c...
Y no es un sistema de ecuaciones...
-

Luis Angel
el 14/4/16Primeros tienes ln{tgx(x/2)}, utiliza d/dx ln u = u'/u luego tienes cotgx . ln (1+senx) ---> multiplicación de funciones u.v = u'.v +u.v' ---> teniendo en cuenta lo siguiente; d/dx cotgx = -csc^2x y d/dx ln u = u'/u, claro lo tienes todo en una sola derivada pero puedes hacerlas paso a paso y luego lo ordenas todo













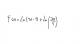

_Thumb.jpg)



_Thumb.png)



_Thumb.jpg)
