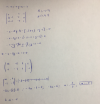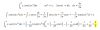-


Breaking Vlad
el 27/1/20se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)
-
x-y+az=-1 Ese es mi sistema, y para que sea SCD determine a≠0 v a≠1/2
ax+2ay-z=0 Cuanto seria "y" en este caso?-2x+2y-z=2b
-
necesito ayuda para este problema no entiendo muy bien...
tengo un problema para llenar de agua una piscina hay tres surtidores . El primer surtidor tarda 30 horas en llenarla, el segundo tarda 40 horas y el tercero tarda 120 horas . si los tres surtidores se conectan juntos ¿Cuanto tiempo tarda la piscina en llenarse?
-


Jose Ramos
el 24/1/20El argumento análogo sería:
Calculo un plano genérico paralelo a las dos rectas. (con el producto vectorial de los vectores de ambas rectas obtengo el vector normal del plano). Ya tendríamos el plano buscado salvo el término independiente D. Para hallar D impones la condición de que la distancia P al plano es 2 y de ahí se despeja D, que te dará dos posibles soluciones.
-


Antonio Silvio Palmitano
el 24/1/20Tienes la expresión de la función:
f(x) = Ln(x)/√(x), cuyo dominio es: D = (0;+∞).
Luego, escribes la expresión de la función como una multiplicación (observa que expresamos a la raíz como una potencia con exponente fraccionario, y que aplicamos la propiedad de las potencias con exponentes negativos), y queda:
f(x) = Ln(x)*x-1/2,
aquí derivas (observa que debes aplicar la Regla de una Multiplicación de funciones), y queda:
f ' (x) = x-1*x-1/2 + Ln(x)*(-1/2)*x-3/2,
aplicas la propiedad de una multiplicación de potencias con bases iguales en el primer término, resuelves el signo y el coeficiente en el segundo término, y queda:
f ' (x) = x-3/2 - (1/2)*Ln(x)*x-3/2,
extraes factores comunes (1/2 y x-3/2), y queda:
f ' (x) = (1/2)*x-3/2*(2 - Ln[x]),
aplicas la propiedad de las potencias con exponentes negativos en el segundo factor, y queda:
f ' (x) = (1/2)*(1/x3/2)*(2 - Ln[x]),
aplicas la propiedad de las potencias con exponentes fraccionarios en el segundo factor, resuelves la multiplicación de los dos últimos factores, y queda:
f ' (x) = (1/2)*( (2 - Ln(x])/√[x3] ) (1),
y observa que la función derivada primera está definida en todo el dominio de la función.
Luego, planteas la condición de punto estacionario, y queda la ecuación:
f ' (x) = 0,
sustituyes la expresión de la función derivada señalada (1) en el primer miembro, y queda:
(1/2)*( (2 - Ln(x])/√[x3] ) = 0,
multiplicas por 2 en ambos miembros, y queda:
(2 - Ln(x])/√[x3] = 0,
multiplicas por √[x3] en ambos miembros (observa que esta expresión no toma el valor cero en el dominio de la función), y queda:
2 - Ln(x] = 0,
restas 2 en ambos miembros, y queda:
-Ln[x] = -2,
multiplicas por -1 en ambos miembros de esta ecuación, y queda:
Ln[x] = 2,
compones en ambos miembros con la función inversa de la función logarítmica natural, y queda:
x = e2,
que es un valor que pertenece al dominio de la función.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 24/1/20a)
Tienes planteada la ecuación cartesiana implícita del plano π, a partir de la cuál tienes que la expresión de uno de sus vectores normales es:
n = < m ; -6 ; 2 > (1).
Tienes las ecuaciones cartesianas paramétricas del plano π', a partir de la cuál tienes dos vectores pertenecientes a dicho plano:
u' = < 1 ; -1 ; -2 > (asociado al parámetro λ) y v' = < 1 ; 0 ; 1 > (asociado al parámetro μ),
y como estos dos vectores no son paralelos (te dejamos la tarea de verificarlo), planteas que un vector normal a este plano es el producto vectorial de los vectores u' y v' pertenecientes a él, y queda:
n' = < -1 ; -3 ; 1 > (2).
Luego, puedes plantear la condición de perpendicularidad entre los planos π y π' (el producto escalar de sus vectores normales es igual a cero), y queda la ecuación vectorial:
n' • n = 0, sustituyes las expresiones de los vectores, y queda:
< -1 ; -3 ; 1 > • < m ; -6 ; 2 > = 0, desarrollas el producto escalar, y queda:
-1*m - 3*(-6) + 1*2 = 0, resuelves términos numéricos, y luego despejas:
m = 20, que es el valor para el cuál los planos π y π' son perpendiculares.
Luego, puedes plantear la condición de paralelismo entre los planos π y π' (el producto vectorial de sus vectores normales es igual al vector nulo), y queda la ecuación vectorial:
n' x n = O, sustituyes las expresiones de los vectores, y queda:
< -1 ; -3 ; 1 > x < m ; -6 ; 2 > = < 0 ; 0 ; 0 >, desarrollas el producto vectorial, y queda:
< 0 ; m+2 ; 3*m+6 > = < 0 ; 0 ; 0 >, por igualdad ente expresiones vectoriales igualas componente a componente, y queda:
0 = 0, que es una Identidad Verdadera,
m + 2 = 0, de donde despejas: m = -2,
3*m + 6 = 0, de donde despejas: m = -2,
por lo que puedes concluir que m = -2, es el valor para el cuál los planos π y π' son paralelos.
Luego, puedes concluir que los planos π y π' son secantes para todo número real m que sea distinto de -2 y distinto de 20.
Espero haberte ayudado.
-
Tengo una pequeña duda.... cuando me piden hallar valores estacionarios de una funcion es lo mismo que decir puntos criticos?
Se q los puntos criticos son los valores donde hace q la derivada sea cero no se si estoy equivicada o que .... desde ya gracias!
-