-
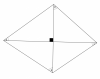
Hola, me pueden explicar como resolver este problema utilizando geometría. Sé que en estos tipos de problemas se tiene que crear un cuadrilátero inscriptible.
Hallar "x". Si: α = 36°; β = 18°; θ = 78°
Muchas gracias
-
Creo que en sus notas hay un pequeño error al comienzo de la ecuación, que convierte el final de la ecuación en la respuesta incorrecta. Todo el problema no está en el estilo de resolver su ecuación, sino en los conceptos básicos que nos enseñan en la escuela. Recientemente tuve problemas similares en un sistema de ecuaciones matriciales. Incluso tuve que contratar a un tutor de https://buscatuprofesor.es/ , que una vez más me explicó con lucidez cómo resolver ecuaciones matriciales. A veces vale la pena actualizar su conocimiento, porque tendemos a olvidar mucho.
-
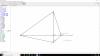
 4ºESO, sistema de inecuaciones con dos incógnitas.
4ºESO, sistema de inecuaciones con dos incógnitas.Buenas noches. En el día de ayer os planteé una duda sobre el adjunto ejercicio. La de hoy es distinta. Se refiere a cómo definir con la mayor exactitud posible en términos matemáticos (si es que fuera factible en este problema) la solución de la inecuación, teniendo en cuenta que existen dos condicionantes que, si los incluyese en el gráfico, ya no estaríamos hablando de un sistema de inecuaciones con dos incógnitas, sino con cuatro. He escrito parcialmente la solución. Personalmente me temo que no es posible, aunque si se pudiera mejorar ya merecería la pena para mí. Lamento daros tanto trabajo. Gracias de antemano.
-


Antonio Silvio Palmitano
el 23/1/20Aquí planteas la ecuación cartesiana explícita genérica de una parábola, y queda:
y = a*x2 + b*x + c = 0 (1), con los coeficientes a, b, c que son números reales, y con a distinto de cero.
Luego, reemplazas las coordenadas del punto A(1,-1) en la ecuación de la parábola señalada (1), resuelves coeficientes, y queda:
-1 = a + b + c (2).
Luego, reemplazas las coordenadas del punto B(0,1) en la ecuación de la parábola señalada (1), resuelves coeficientes, cancelas términos nulos, y queda:
1 = c.
Luego, reemplazas las coordenadas del punto C(2,2) en la ecuación de la parábola señalada (1), resuelves coeficientes, y queda:
2 = 4*a + 2*b + c (3).
Luego, reemplazas el valor remarcado en la ecuación señalada (1) y en la ecuación señalada (3), y quedan las ecuaciones:
-1 = a + b + 1, aquí restas 1 y restas a en ambos miembros, y queda: -2 - a = b (4),
2 = 4*a + 2*b + 1, aquí restas 1 en ambos miembros, y queda: 1 = 4*a + 2*b (5).
Luego, sustituyes la expresión señalada (4) en el último término de la ecuación señalada (5), y queda:
1 = 4*a + 2*(-2 - a), distribuyes el último término, reduces términos semejantes en el segundo miembro, y queda:
1 = 2*a - 4, aquí sumas 4 en ambos miembros, y queda: 5 = 2*a, divides por 2 en ambos miembros, y queda. 5/2 = a.
Luego, reemplazas este último valor remarcado en la ecuación señalada (4), resuelves, y queda: -9/2 = b.
Luego, reemplazas los valores de los coeficientes que tienes remarcados en la ecuación de la parábola señalada (1), y queda:
y = (5/2)*x2 - (9/2)*x + 1,
que es la ecuación cartesiana explícita de la parábola que pasa por los tres puntos que tienes indicados en tu enunciado.
Espero haberte ayudado.
-
hola me puedes ayudar con este ejercicio de integracion por partes, mi duda es el valor que toma el valor de C en la funcion o corroborar el ejercicio que he hecho. muchas gracias


Antonio Silvio Palmitano
el 23/1/20Tienes los datos:
V(0) = 0,5 dm3 (volumen inicial de líquido),
R(t) = (t + 1)*e-0,2*t (razón de introducción de toxina, en mL/min),
C(0) = 0,5 mL/dm3 (concentración inicial de toxina),
t = 0 (instante inicial de agregado de toxina),
t = 20 min (instante final de agregado de toxina).
1°)
Comienzas por plantear el volumen inicial de toxina:
V(0) = C(0)*V = 0,5*0,5 = 0,25 mL (1).
Luego, planteas la expresión del volumen agregado de toxina durante los veinte minutos que dura el experimento, y queda:
ΔV = 0∫20 (t + 1)*e-0,2*t*dt (2).
Luego, planteas la expresión del volumen total de toxina al finalizar el experimento, y queda:
V(20) = V(0) + ΔV (3).
2°)
Planteas la integral indefinida correspondiente a la integral señalada (2), y queda:
∫ (t + 1)*e-0,2*t*dt =
aplicas el Método de Integración por Partes:
u = t + 1, de donde tienes: du = dt,
dv = e-0,2*t, de donde tienes: v = e-0,2*t/(-0,2) = -5*e-0,2*t,
aplicas el método, extraes el factor constantes de la integral secundaria, y queda:
= (t + 1)*e-0,2*t + 5*∫ e-0,2*t*dt =
resuelves la integral secundaria, y queda;
= (t + 1)*e-0,2*t + 5*e-0,2*t/(-0,2) + C =
= (t + 1)*e-0,2*t - 25*e-0,2*t + C =
= (t + 1 - 25)*e-0,2*t + C =
= (t - 24)*e-0,2*t + C (4).
3°)
Planteas la integral definida señalada (2), y queda (indicamos con corchetes que debes evaluar con Regla de Barrow):
ΔV = 0∫20 (t + 1)*e-0,2*t*dt =
evalúas (observa que sustituimos la expresión señalada (4) y que omitimos la constante de integración), y queda:
= [ (t - 24)*e-0,2*t ] =
evalúas para los límites de integración (0 y 20), y queda:
= -4*e-4 - (-24) =
= 24 - 4*e-4 mL (5).
4°)
Reemplazas los valores señalados (1) (5) en la expresión del volumen final de toxina señalada (3), y queda:
V(20) = 0,25 + 24 - 4*e-4,
reduces términos racionales, y queda:
V(20) = 24,25 - 4*e-4 mL.
Espero haberte ayudado.