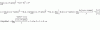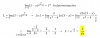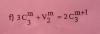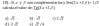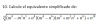-
Saludos,
¿Cómo puedo resolver limites por el método de sustitución de variables que llevan racionalización con indices cúbicos o mayores a 3 y valor absoluto?
-Por el método de sustitución los ejercicios 20 al 24 (excepto el 22).
-Por valor absoluto 25 y 26.
Espero que puedan ayudarme :)
Lamentablemente no le entiendo a mi profe, tampoco a explicado este tipo de ejercicios los cuales para mi están complejos. He buscado vídeos de alguna explicación de estos tipos de límites pero no he tenido suerte :c
Se les agradecería infinitamente a quien sea mi salvador del semestre :D


Diego Fernando
el 16/2/20tengo una pregunta para Jose Ramos. Más precisamente en el ejercicio 20.
Como sabes que t tiende a 1? es porque en ese punto se indetermina? o utilizas una regla? es decir cuando hago el cambio de variable siempre la variable que tome va a tender al punto donde se indetermine?. Así es?. Saludos
-
No quiero quedar como flojo por hacer 2 preguntas seguidas del mismo tema. Se que me falta algebra... pero serian de gran ayuda si me dan una mano con este ejercicio. Sucede que en otros ejercicios similares logro hallar la "m" descomponiendo. Pero en este particular no me sale.
(Analisis combinatorio)
-
Hola. Tengo un pequeño follón con los tipos de discontinuidades. Si los límites laterales existen y son iguales, pero es distinto al valor de la función ¿qué tipo de discontinuidad sería?. Mil gracias.

César
el 15/2/20Aqui recopiladas las discontinuidades
https://es.wikipedia.org/wiki/Clasificaci%C3%B3n_de_discontinuidades
-
Hola, como resuelvo esto. Me estuve partiendo la cabeza, intentadole de todos los lados y no puedo hallar el valor correcto de "m". (Analisis Combinatorio) (C: Combinación; V: Variación)
Seria de gran ayuda si alguien me puede echar una mano. Desde ya gracias.



Antonio Silvio Palmitano
el 14/2/20Resuelves la división de expresiones en el primer miembro, y queda:
6!*C(m,5)/V(m,6) = 2/3 (1).
Luego, planteas las expresiones:
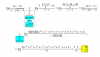
C(m,5) = m!/[5!*(m-5)!] (2),
V(m,6) = m!/(m-6)! (3);
luego, divides miembro a miembro la ecuación señalada (2) entre la ecuación señalada (3), resuelves, simplificas, y queda:
C(m,5)/V(m,6) = (m-6)!/[5!*(m-5)!], expresas como una multiplicación de expresiones fraccionarias, y queda:
C(m,5)/V(m,6) = (1/5!)*[(m-6)!/(m-5)!], simplificas en el último factor (recuerda: (m-5)! = (m-5)*(m-6)!), y queda:
C(m,5)/V(m,6) = (1/5!)*[1/[m-5)] (4).
Luego, sustituyes la expresión señalada (4) en lugar de la expresión fraccionaria que tienes remarcada en la ecuación señalada (1), y queda:
6!*(1/5!)*[1/[m-5)] = 2/3, simplificas entre los dos primeros factores los factoriales numéricos (recuerda: 6! = 6*5!), y queda:
6*[1/[m-5)] = 2/3, divides por 2 y multiplicas por 3 en ambos miembros, y queda:
9*[1/[m-5)] = 1, resuelves el primer miembro, y queda:
9/(m-5) = 1, multiplicas por (m-5) en ambos miembros, y queda:
9 = m - 5, y de aquí despejas:
m = 14.
Queda para ti que verifiques la validez de la solución remarcada.
Espero haberte ayudado.