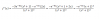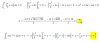-


Breaking Vlad
el 24/1/20se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)


Fatima
el 24/1/20Buenas tardes, tiene razón y de hecho solo subo ejercicios después de haberlos intentado resolver. En mi caso no voy a clases, estudio a distancia y solo nos proporcionan un pdf y me resulta muchísimo más complicado resolver ejercicios de matemáticas de esta forma. De no haberlo intentado no subiría el enunciado y ya he visto videos relacionados con el ejercicio y aún así no logro resolverlo. Espero que lo entienda, un saludo, gracias.

Sebastián Bustamante López
el 24/1/20Lo primero es resolver las Integrales por decir de una forma "ignorando en la uno el 9", lo desarrolle y obtendras una ecuacion de segundo grado la cual igualas al 9, con eso ya puedes utilizar la formula general para obtener los valores de a, saludos. Si no lo logras avisame.
-
Contestarme lo ante posible
En una urna hay 4 bolas blancas y una negra. Se extraen sucesivamente 2 bolas sin reemplazamiento.
La probabilidad de que las dos bolas sean negras es
La probabilidad de que las dos sean blancas es
La probabilidad de que la segunda sea blanca si la primera sale negra es
-
Ayudarme
La probabilidad de que un alumno de 2º BACH vaya de viaje de fin de curso si no titula es 0,15 y la probabilidad de que titule es 0,6. ¿Cuál es la probabilidad de que no titule y se vaya de viaje de fin de curso?


Breaking Vlad
el 24/1/20se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)
-
Contestarme lo ante posible
En una urna hay 4 bolas blancas y una negra. Se extraen sucesivamente 2 bolas sin reemplazamiento.
La probabilidad de que las dos bolas sean negras es
La probabilidad de que las dos sean blancas es
La probabilidad de que la segunda sea blanca si la primera sale negra es
La probabilidad de que las dos sean de diferente color es
-
Ayudarme por favor
En una caja hay bolígrafos rojos y azules. El 25% son rojos
y el resto azules. El 10% de los rojos y el 20% de los azules no escriben
porque tienen la tinta gastada. Se elige un bolígrafo al azar.
Resuelve cada una de las
siguientes situaciones:
¿Cuál es la probabilidad de que escriba si se sabe que es
azul?
¿Cuál es la probabilidad de que funcione correctamente?
¿Cuál es la probabilidad de que sea rojo y no le quede
tinta?
Si es rojo, ¿cuál es la probabilidad de que no escriba?
¿Cuál es la probabilidad de que no escriba?
¿Cuál es la probabilidad de que no sea rojo?