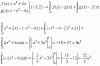-


Antonio Silvio Palmitano
el 21/1/20Tienes la expresión del valor de la vivienda en función del tiempo:
V(t) = k*ea*t (1),
con t expresado en años, y con V expredado en euros;
y tienes también las condiciones:
V(0) = 350000 (2) (este es el precio inicial de la vivienda),
V(5) = 225000 (3) (este es el valor luego de transcurridos cinco años desde la compra de la vivienda.
a)
Planteas la condición señalada (2), y queda:
V(0) = 350000, sustituyes la expresión de la función señalada (1) evaluada en el primer miembro, y queda:
k*ea*0 =350000, resuelves el coeficiente en el primer miembro, y luego despejas:
k = 350000.
Luego, planteas la condición señalada (3), y queda:
V(5) = 225000, sustituyes la expresión de la función señalada (1) evaluada en el primer miembro, y queda:
k*ea*5 = 225000, reemplazas el valor que tienes remarcado en el primer miembro, y queda:
350000*ea*5 = 225000,divides por 350000 en ambos miembros, simplfificas, y queda:
ea*5 = 9/14, compones en ambos miembros con la función inversa de la función exponencial natural, y queda:
a*5 = Ln(9/14), divides por 5 en ambos miembros, y queda:
a = Ln(9/14)/5, resuelves el segundo miembro (aquí es conveniente consignar al menos cuatro cifras decimales), y queda:
a ≅ -0,088367,
Luego, reemplazas los dos valores remarcados en la expresión de la función señalada (1), y queda:
V(t) ≅ 350000*e-0,088367*t (4).
b)
Tienes el valor de la vivienda en estudio:
V(t) = 350000/3, sustituyes la expresión de la función que tienes remarcada y señalada (4) en el primer miembro, y queda:
350000*e-0,088367*t≅ 350000/3, divides por 350000 en ambos miembros, y queda:
e-0,088367*t≅ 1/3, compones en ambos miembros con la función inversa de la función exponencial natural, y queda:
-0,088367*t ≅ ln(1/3), aplicas la propiedad del logaritmo del recíproco de un número en el segundo miembro, y queda:
-0,088367*t ≅ -ln(3), diides en ambos miembros por -0,088367, y queda:
t ≅ ln(3)/0,088367, resuelves el segundo miembro, y queda:
t ≅ 12,432445 años ≅ 12,4 años.
Espero haberte ayudado.
-
Hola! otro ejercicio de probabilidad:
En una clase hay 30 alumnos y debemos escoger un Delegado, un Subdelegado y un Suplente. ¿Cuál es la probabilidad de que mi amigo Pedro, Cristina y yo mismo seamos los elegidos para alguno de los 3 puestos?
Saludos!
-
Hola! Mando un ejercicio de probabilidades. Pediría resolverlo en forma de árbol y también usando la probabilidad condicionada si se puede. Ahí va:
Tenemos una urna con 4 bolas blancas, 7 de negras y 9 de rojas. Escogemos una bola al azar, anotamos el color y la volvemos a poner dentro de la urna. Extraemos una segunda bola al azar. Se pide:
a) Probabilidad de haber sacado 2 bolas negras
b) Probabilidad de haber sacado 1 bola roja y 1 bola blanca, en este orden
Gracias!!
-
Considera el polinomio p(x) = -4·(x-b)2·(x-4). Sabemos que el coeficiente del término de grado 1 de la derivada de este polinomio es - 32. ¿Cuál es el valor de b?
Alguien me podrías orientar como saber le valor de B? GraciasP.D: (x-B) es elevado a dos


Antonio Silvio Palmitano
el 20/1/20Vamos con la idea del colega Rubén.
Planteas la expresión de la derivada de la función polinómica (observa que debes aplicar la Regla de una Multiplicación de Funciones), y queda:
p'(x) = -8*(x - b)*(x - 4) - 4*(x - b)2 (*), desarrollas esta expresión, y queda:
p'(x) = -8*x2 + 32*x + 8b*x - 32b - 4*x2 + 8b*x - 4b2, reduces términos semejantes, y queda:
p'(x) = -12*x2 + 32*x + 16b*x - 32b - 4b2,
asocias y extraes factor común con los términos lineales, asocias y extraes factor común con los términos constantes, y queda:
p'(x) = -12*x2 + (32 + 16b)*x - (32b + 4b2).
Luego, tienes en tu enunciado el valor correspondiente al coeficiente del término lineal (-32), por lo que puedes plantear la ecuación:
32 + 16b = -32, y de aquí despejas:
b = -4.
Luego, puedes sustituir este valor remarcado en la expresión de la función que tienes en tu enunciado, luego desarrollarla, luego derivarla, y comprobar que el coeficiente del término lineal de esta última expresión es -32 (te dejo la tarea).
Espero haberte ayudado.
-
Hola, tengo duda con este ejercicio en cuanto a la parte de la gráfica que viene como respuesta, o creo que son las secciones. Alguien me puede decir cómo es que se hizo porque no consigo verlo.




David
el 29/1/20Hola! Me encantaría ayudarte, pero no respondemos dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
Imaginen que nos dan una aplicación lineal f:ℛ³-->ℛ² definida por ejemplo como f(x,y,z)=(x+y,x-z) respecto de unas bases B3 y B2 diferentes a la base canónica:
1.- ¿Cuántas y qué formas distintas existen para hallar la matriz asociada a la aplicación f respecto de las bases B3 y B2?
2.- ¿Si multiplicamos dicha matriz asociada por un elemento u de ℛ³ nos dará un elemento v de ℛ² pero, es este último el mismo que si hacemos f(u) usando cómo está definida f o solo será el mismo si la matriz está asociada a f respecto de la base canónica?


Breaking Vlad
el 24/1/20Hola! Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
Hola buenos días, estaba resolviendo ejercicios y este me pareció raro porque da dos bases pero le asigna el mismo nombre y aparte dice que use el calculo integral y solo conozco de hacerlo con matrices haciendo uso de la base canónica, me podrían decir como se procede o proporcionarme un ejemplo por favor