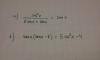-
Buen días amigos, por favor me podrían ayudar con estos ejercicios o en su defecto proporcionar algún material para resolverlos
1- Calcular el área cerrada entre la gráfica de la recta y la parábola dada (recta f(x) = x ; g(x) = x2)
2- Calcular el área de la región comprendida entre la gráfica parábola (f(x)=x2 y(x)= -x2 +2)
3- Calcular el área cerrada entre la gráfica función x y eje horizontal (f(x)=xsenx ; 0 ≤ x ≤ 2π )
4- Calcular el área entre la gráfica de la función definida atroso (f(x) = ΙxΙ ; -2≤ΙxΙ≤2
5- Calcular el área cerrada ebtre la gráfica de una función polinómica de 4to grado y el eje de las abcisas (recta x=0 y x=7; F(x)= x(x-1)(x-3)(x-6)
6- Se suelta un pequeño globo a 150 pues con respecto a un obsevador que está a nivel del suelo, si el globo se eleva verticalmente a una velocidad de 8 pies/segundos con ¿Qué rapidez aumenta la distancia del observador al globo cuando se halle a 50 pues de altura? (me comentan el uso de pitagoras y ecuación diferencial)
-


Breaking Vlad
el 20/1/20se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)










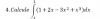




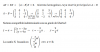




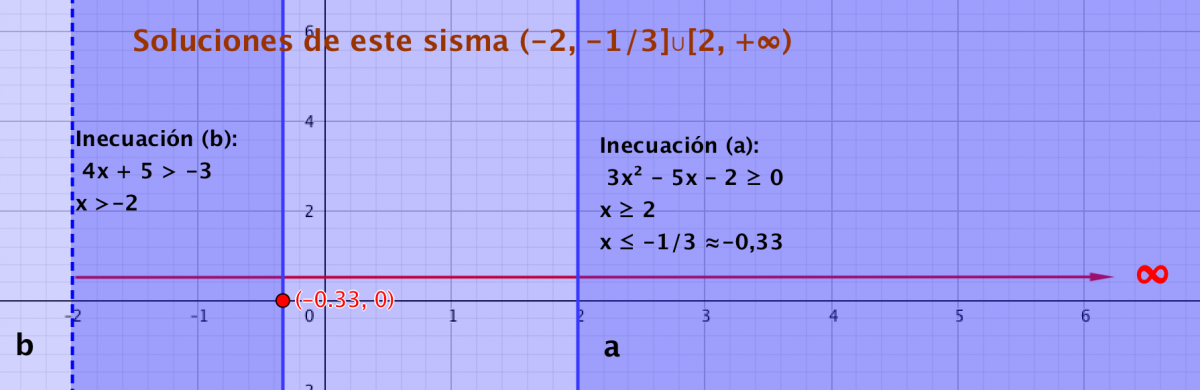 Muchas gracias Jose. Todavía me sigo haciendo un poco de lío con esto. Ahora entiendo este ejercicio. Me ha costado un poco visualizar las “soluciones comunes a ambas” Tengo que practicar más. Veamos cómo se me dan los sistemas con dos ecuaciones, que es el paso siguiente.
Muchas gracias Jose. Todavía me sigo haciendo un poco de lío con esto. Ahora entiendo este ejercicio. Me ha costado un poco visualizar las “soluciones comunes a ambas” Tengo que practicar más. Veamos cómo se me dan los sistemas con dos ecuaciones, que es el paso siguiente.