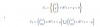-
 en el ejercicio 19 debo insertar los valores de las coordenadas en la matriz?. Hacer gauss,y resolver el sistema para que me de un sistema compatible determimado?.
en el ejercicio 19 debo insertar los valores de las coordenadas en la matriz?. Hacer gauss,y resolver el sistema para que me de un sistema compatible determimado?.

David
el 19/1/20Te dicen una cosa muy importante en el enunciado: es SCD. ¿Qué quiere decir eso?
Que el rango de la matriz y la ampliada es 3. Hacer Gauss es una solución, pero de cara a hacer cero la posición a32 de la matriz te va a costar más de lo habitual. Se me ocurre aplicar Cramer (no me he puesto a hacerlo y no sé si será lo más práctico en este ejercicio), por la condición SCD.
-


Breaking Vlad
el 20/1/20se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)