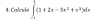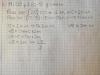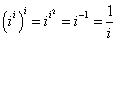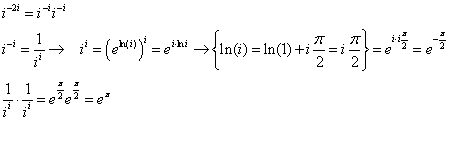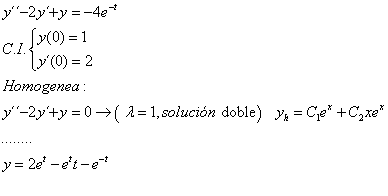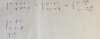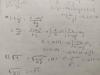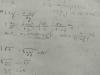-


Breaking Vlad
el 20/1/20se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)
-


Antonio Silvio Palmitano
el 18/1/20Aquí integras término a término, y la integral definida de tu enunciado queda (observa que indicamos con corchetes que debes evaluar con Regla de Barrow):
I = [ x + 2x2/2 - 3x3/3 + x4/4 ], simplificas en el segundo término y en el tercer término, y queda:
I = [ x + x2 - x3 + x4/4 ], evalúas, y queda:
I = ( (1) + (1)2 - (1)3 + (1)4/4 ) - ( (-1) + (-1)2 - (-1)3 + (-1)4/4 ), resuelves términos en los agrupamientos, y queda:
I = ( 1 + 1 - 1 + 1/4 ) - ( -1 + 1 - 1 + 1/4 ), reduces términos semejantes (observa que tienes cancelaciones) y resuelves en los agrupamientos, y queda:
I = 5/4 - ( -3/4 ), resuelves, y queda:
I = 2.
Espero haberte ayudado.
-
Hola, en esta ecuación diferencial de 2 orden no entiendo (punto 4) como sacar la derivada y como sacar el dato inicial a partir de esta (y'=0) por favor alguien me puede guiar. Gracias.

-
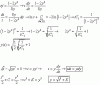
Buenos días David! Una pregunta que me hace pensar bastante aunque creo que es una tontería. ¿Porque en ocasiones la desviación típica no es solo esta, sino la desviación típica dividida entre la raíz cuadrada de n(tamaño muestral)?. ¿Cómo lo puedo identificar en un ejercicio de distribución normal, para saber si a lo largo del ejercicio tengo que usar la desviación típica o la división entre esta y la raíz cuadrada de n?. Muchas gracias por tu atención y un enorme abrazo por todo lo que haces, una gran labor. Un fuerte saludo desde Madrid crack!!


Jose Ramos
el 18/1/20La diferencia está en que trabajes con la población o con la muestra. Cuando calculas la media de una muestra, la variable aleatoria "media de X" tiene de esperanza la media de la población. Sin embargo la desviación típica muestral no coincide con la desviación típica poblacional, sino que la desviación típica muestral es la desviacion típica poblacional dividido por √n, donde n es el tamaño de la muestra. Te lo demuestro a continuación con la media y la desviación típica:
-