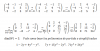-
Sean P = (4, 9), Q = (−6, 5) y L : X = λ.(1, 2). Hallar todos los puntos R ∈ L
tales que:
a) el triángulo PQR sea rectángulo en P.
b) el triángulo PQR sea rectángulo en R.


Breaking Vlad
el 20/1/20se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)
-


Breaking Vlad
el 20/1/20se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)
-
Hola tengo dudas con este ejercicio:
La población de ciertos primates sigue la función P(t) = a+ t/et/2 . Donde P(t) es el número de la población medido en miles y t el tiempo medido en meses y a es una constante positiva
a) Calcular "a" sabiendo que inicialmente había 3000 primates
b) ¿A que tiende la población en el futuro?
c) Si se sabe que la población esta en peligro de extinción cuando el numero es menor que 1000, ¿tiene peligro de extinción esta población?
Lo que he hecho
a) Como habia 3000 primates inicialmente y como esta en miles. P(t) = 3 en t=0 ya que inicialmente el tiempo es cero.
Reemplazando
3=a+0/e0/2
3=a+0/e0
3=a
b) Para esto tenemos que calcular el limite de la función cuando t tiende a infinito es decir lim (t --> ∞) 3+t/et/2 (que no se resolver paso a paso) (aqui tengo mis dudas pero creo que es 3)
De anteano gracias
-
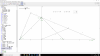
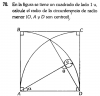
 4ºESO inecuación de primer grado con dos incógnitas. Gráfica y soluciones de (5x - 6y ≤ 0).
4ºESO inecuación de primer grado con dos incógnitas. Gráfica y soluciones de (5x - 6y ≤ 0).Buenas noches. En las inecuaciones de primer grado con una sola incógnita sé como reflejar la solución al tratarse de intervalos. Sin embargo no sé si existe una forma general de expresar la solución, o soluciones, en las de primer grado con dos incógnitas. Adjunto imagen de ejercicio, y su gráfica realizado con GG. Gracias de antemano.
-


Breaking Vlad
el 20/1/20se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)