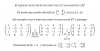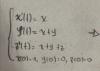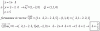-
Buenas, la duda que tengo es porque en algunas ecuaciones trigonométricas, sólo tienen una única solución como es el caso de 2tg4x=1
- x= (26,56º+180º.k)/4 la tagente es positiva en el 3º cuadrante y por qué en ese cuadrante no es solución y la otra duda que tengo porque se coge media vueltas de grados es decir se pone 180º.K. Y como puedo diferenciar cuando tiene una única solución o dos soluciones. Muchas gracias de antemano por su tiempo. Un cordial saludo


Jose Ramos
el 15/1/20Resulta que la tangente tiene periodo 180º, entonces cuando llegas a tag 4x = 1/2, el menor ángulo que lo verifica está en el primer cuadrante es 26,56º. Como el periodo es 180º vas añadiendo de 180 en 180, es decir le sumas 180k. Si k = 1 ya obtienes el ángulo en el 3º cuadrante que es la otra solución en la primera vuelta. De ahí que no haya que mencionar dicho ángulo (sin embargo en el seno y el coseno esto no ocurre porque el periodo des 360º, por lo que hay que mencionar los dos ángulos solución y sumarles 360 k).
Espero que te haya quedado claro.
- x= (26,56º+180º.k)/4 la tagente es positiva en el 3º cuadrante y por qué en ese cuadrante no es solución y la otra duda que tengo porque se coge media vueltas de grados es decir se pone 180º.K. Y como puedo diferenciar cuando tiene una única solución o dos soluciones. Muchas gracias de antemano por su tiempo. Un cordial saludo
-


Breaking Vlad
el 15/1/20Se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado, pero no olvidéis de adjuntarlo de forma LITERAL, para saber que os piden. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)
-
Buenas unicoos, me ayudab con esta integral x favor. Sé que es una sustitución trigonométrica pero no me sale.


Alejandro Legaspe
el 15/1/20Observa que 9x²+6x-8=(3x+1)²-9,si construyes un triangulo rectangulo tal que un segmento de longitud √[(3x+1)²-9] se oponga al un angulo α y un segmento de longitud 3 sea el cateto adyacente a ese angulo α de tal forma que la hipotenusa sea 3x+1,tenemos entonces que cosα=3/(3x+1),así x=secx-1/3,por lo que dx=secα tgα dα
Por otro lado,con esta construcción,se tiene que √[9x²+6x-8]=√[(3x+1)²-9]=3tgα,así,haciendo el cambio de variable,tenemos que la integral que tienes puede cambiarse a la siguiente integral
∫(secα tgα dα)/ 3tgα=(1/3)∫secα dα=(1/3)Ln|secα+tgα|+C
Deshaciendo el cambio,tenemos que secα=x+1/3 y que tgα=√[(3x+1)²-9] / 3,así,tenemos que el resultado de la integral otiginal es:
(1/3) Ln|x+1/3+√[(3x+1)²-9] / 3|+C
Cualquier duda,quedo atento
-


Alejandro Legaspe
el 15/1/20Para W={f|f(1)=f(7)} es fácil ver que la función idénticamente (Denotemosla por 0(x),así 0(x)=0 ∀x∈ℛ) está en W,es decir 0(x)∈W pues 0=0(1)=0(7)=0 (Observa que la función 0(x) es el elemento neutro aditivo del espacio vectorial V)
Ahora bien,si definimos la suma de funciones reales de forma usual,es decir si f y g son funciones de ℛ en ℛ,definimos de forma usual la suma de funciones como la función de ℛ en ℛ,cuya regla de correspondencia está descrita de la siguiente manera:
(f+g)(x)=f(x)+g(x)
Es fácil ver que si dos funciones están en W,la suma de las mismas también esta en W,pues sean f y g dos funciones que están en W,así,tenemos que,por un lado, f(1)=f(7) y por otro que g(1)=g(7)
Además,observa que,por la definición de la suma de funciones y usuando lo anterior,tenemos que
(f+g)(1)=f(1)+g(1)=f(7)+g(7)(f+g)(7)
Así,tenemos que (f+g)∈W
Por último,si definimos el producto por un escalar (Sin pérdida de generalidad,supongamos que V es un ℛ-espacio vectorial) para α∈ℛ y f∈W de forma usual,es decir que la función αf sea una función de ℛ en ℛ cuya regla de correspondencia queda descrita del siguiente modo:
(αf)(x)=α f(x)
Tenemos entonces que,si α∈ℛ y f∈W (Esto es que f(1)=f(7)),por la definición del producto,tenemos
(αf)(1)=α f(1)=α f(7)=(αf)(7)
Es decir,(αf)(x)∈W así,hemos probado que W es un subespacio vectorial de V.
Para el otro ejercicio observa que la función idénticamente cero (Que la llamamos 0(x)) es el neutro aditivo de V,sin embargo,0(x)∉W pues observa que 0(7)=0 yt por otro lado 2+0(1)=2+0=2 así,no es cierto que 0(7)=2+0(1) por lo que W no es subespacio vectorial de V.
Cualquier duda,quedo atento