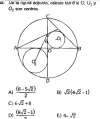
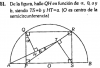
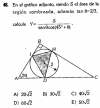
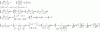-

Antonio
el 11/1/20Pasa las ecuaciones dadas a forma paramétrica:
para ello buscaremos en cada una de ellas un vector director y un punto:
En la recta r tenemos v→=(-5,4,3) y P=(-1,1,0) y en la recta s tenemos u→=(1,-1,-1) y Q=(0,0,a); por lo que:
x=-1-5λ x=μ
r≡ y=1+4λ s≡ y=-μ
z=3λ z=a-μ
ahora igualamos:
-1-5λ=μ
1+4λ =-μ
3λ=a-μ
de las dos primeras obtenemos que λ=0 ^ μ=-1
y de la tercera que a=-1
siendo el punto de corte (-1,1,0)
-


Breaking Vlad
el 13/1/20se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)
-


Breaking Vlad
el 13/1/20se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)
-


Breaking Vlad
el 13/1/20se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)
-
Por favor , ¿ me puede ayudar alguien a resolver este problema?
Hallar el ángulo que forma la recta 3x- y+ 11 = 0 con los ejes de coordenadas.
Gracias


Jose Ramos
el 11/1/203x+y-11=0 tiene como vector director (-1,3) y el eje X tiene como vector (1,0). El ángulo que forman ambos vectores es arccos{ (-1,3).(1,0)/√10.√1} = arccos -1/√10 = 108,43º o 71,57º
3x+y-11=0 tiene como vector director (-1,3) y el eje Y tiene como vector (0,1). El ángulo que forman ambos vectores es arccos{ (-1,3).(0,1)/√10.√1} = arccos3/√10 = 161,56º o 18,44º