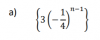-
Hola que tal, quisiera ver si me pudieran ayudar se favor a resolver lo siguiente: Tengo que calcular los angulos complementarios donde
a 1er angulo= 4 veces el segundo + 20 grados
b 2do angulo= 2 veces el tercero - 10 grados
c 3er angulo= cuarto angulo + 20 gredos
d cuarto angulo= x
Segun yo me queda:
4to angulo = x
3er angulo = x+20
Tengo problemas con el segundo y primero.
Gracias.


Antonio Silvio Palmitano
el 11/2/20Vamos con una orientación.
Tienes la expresión de la medida del cuarto ángulo: θ4 = x.
Luego, tienes en tu enunciado que la expresión de la medida del tercer ángulo es:
θ3 = θ4 + 20°, sustituyes la expresión de la medida del cuarto ángulo, y queda: θ3 = x + 20°.
Luego, tienes en tu enunciado que la expresión de la medida del segundo ángulo es:
θ2 = 2*θ3 - 10°, sustituyes la expresión de la medida del tercer ángulo, y queda:
θ2 = 2*(x + 20°) - 10°, distribuyes el primer término de esta expresión, y queda:
θ2 = 2*x + 40° - 10°, reduces términos semejantes, y queda: θ2 = 2*x + 30°.
Luego, tienes en tu enunciado que la expresión de la medida del primer ángulo es:
θ1 = 4*θ2 + 20°, sustituyes la expresión de la medida del tercer ángulo, y queda:
θ1 = 4*(2*x + 30°) + 20°, distribuyes el primer término de esta expresión, y queda:
θ1 = 8*x + 120° + 20°, reduces términos semejantes, y queda: θ1 = 8*x + 140°.
Luego, puedes continuar con la tarea.
Espero haberte ayudado.
-
Hola buenas a todos, me podrían explicar como se hace este ejercicio? Muchas gracias.
Ejercicio: Determinar si esta sucesion converge o diverge.

Antonio Silvio Palmitano
el 11/2/20Tienes la expresión del elemento general de la sucesión:
an = 3*(-1/4)n-1, con n ∈ N, n ≥ 1,
y observa que es la expresión del elemento general de una sucesión geométrica (revisa tus apuntes de clase), cuyos elementos son:
a1 = 3 (primer elemento),
q = -1/4 (razón),
y observa que el valor absoluto de la razón es 1/4, que es menor que 1, por lo que tienes que esta sucesión es convergente.
Luego, planteas la expresión del límite del elemento general, y queda:
Lím(n→+∞) an = Lím(n→+∞) 3*(-1/4)n-1 = 3*Lím(n→+∞) (-1/4)n-1 = 3*Lím(n→+∞) (-1)n-1/4n-1 = 3*0 = 0,
ya que tienes que el numerador en el argumento del límite toma los valores 1 y -1 alternadamente, y el denominador tiende a +infinito.
Espero haberte ayudado.
-
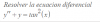
Si a,b y c son numeros racionales tales que:
a+b+c=10
√(a² + 2²) + √(b² + 3²) + √(c² + 5²) = 26
Hallar los valores de a,b y c


Breaking Vlad
el 12/2/20Se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis siempre también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro.
-
Una pregunta muy rápida. ¿Alguien me podría decir como hacer una recta partiendo de estos puntos? P(1,1,-2) , Q(3,-1,4). Es que solo he podido encontrar la fórmula para dos dimensiones y no encuentro la de tres. Por lo que no sé en que varía.
-
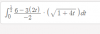
Alguien me puede decir como hacer este problema?
Sea f(x, y) = ... y sea c(t) . Calcular la integral de f sobre los puntos de la curva entre los instantes t 0 0 y t= 1/2.
Lo he intentado hacer mediante la integral de linea y me ha salido esto:
pero esta mal.


Antonio Silvio Palmitano
el 11/2/20Planteas la expresión parametrizada de la función (observa que a partir de la función vectorial correspondiente a la trayectoria tienes: x = 1 - t, y = t2 + 2, con el intervalo paramétrico: 0 ≤ t ≤ 1/2), y queda:
f(c[t]) = (6 - 3*[t2 + 2])/(1 - t - 1), resuelves las expresiones en el numerador y en el denominador, y queda:
f(c[t]) = -3*t2/(-t), simplificas, y queda:
f(c[t]) = 3*t (1).
Planteas la expresión de la función vectorial derivada primera correspondiente a la trayectoria, y queda:
c'(t) = < -1 ; 2*t >, cuyo módulo queda expresado (te dejo el planteo):
|c'(t)| = √(1 + 4*t2) (2).
Luego, tienes la integral de línea de tu enunciado:
I = ∫C f(x,y)*ds, parametrizas, y queda:
I = a∫b f(c[t])*ds,
reemplazas los límites de integración por los valores extremos del intervalo paramétrico, sustituyes las expresiones señaladas (1) (2) en el argumento de la intergral, y queda:
I = 0∫1/2 3*t*√(1 + 4*t2)*dt, extraes el factor constante, ordenas factores, y queda:
I = 3*0∫1/2 √(1 + 4*t2)*t*dt;
luego, integras (observa que debes aplicar la sustitución, o cambio de variable: w = 1 + 4*t2, y que indicamos con corchetes que debes evaluar con Regla de Barrow), y queda:
I = (1/4)*[( √(1 + 4*t2) )3 ],
evalúas, y queda:
I = (1/4)*( ( √(2) )3 - 13 ),
resuelves ambos términos en el agrupamiento (observa: ( √(2) )3 = ( √(2) )2*√(2) = 2*√(2), y 13 = 1), y queda:
I = (1/4)*( 2*√(2) - 1 ), resuelves la multiplicación, y queda:
I = ( 2*√(2) - 1 )/4,
por lo que tienes que la opción señalada (d) es la respuesta correcta.
Espero haberte ayudado.
-
Hola, soy nuevo en la página de unicoos aunque sigo el canal de youtube desde hace bastante tiempo. Estoy estudiando matemáticas por mi cuenta con la esperanza de algún día tener nivel suficiente para sacarme el grado de mates por la UNED. Actualmente estoy con el cálculo, y hay un límite que me trae de cabeza, aunque tengo la solución no se como llegar a ella. Si pudieseis echarme un cable os lo agradecería mucho.

-
Arrojadme luz por favor. Calcular en volumen comprendido entre un cubo y el cilindro que hay en su interior es restar el volumen del cilindro al volumen del cubo, ¿qué pinta el calculo de la esfera en todo esto?