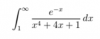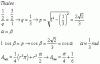-
Buenas, alguien podría resolver y explicarme el siguiente ejercicio. Gracias.
Estudiar la convergencia o divergencia de la integral impropia:


Antonio Silvio Palmitano
el 5/1/20Vamos con una orientación.
Observa que la expresión del argumento de tu integral toma valores estrictamente positivos en el intervalo de integración, ya que tanto la expresión de su numerador como la expresión de su denominador toman también valores estrictamente positivos en dicho intervalo.
Luego, observa que la expresión del denominador toma valores mayores que uno en el intervalo de integración, por lo que tienes que 1 es una cota inferior de dicha expresión.
Luego, puedes plantear la comparación:
e-x/(x4 + 4*x + 1) ≤ minimizamos la expresión del denominador ≤ e-x/1 = e-x (1),
y observa que la expresión señalada (1) toma valores positivos en el intervalo de integración, y que tiende a cero cuando x tiende a +infinito,
por lo que tienes que la expresión del argumento de la integral de tu enunciado también tiende a cero cuando x tiende a +infinito.
Luego, puedes plantear la doble inecuación:
0 < e-x/(x4 + 4*x + 1) ≤ e-x;
luego, con los dos últimos miembros tienes la inecuación:
e-x/(x4 + 4*x + 1) ≤ e-x,
integras en ambos miembros, y queda:
1∫+∞ ( e-x/(x4 + 4*x + 1) )*dx ≤ 1∫+∞ e-x*dx (2),
resuelves la integral impropia del segundo miembro (te dejo la tarea), y queda:
1∫+∞ ( e-x/(x4 + 4*x + 1) )*dx ≤ 1;
y de acuerdo con el Criterio de Comparación, tienes que la integral de tu enunciado es menor o igual que la integral señalada (2), y como esta integral es convergente, entonces tienes que la integral de tu enunciado también lo es.
Espero haberte ayudado.
-
Hola.
Una pregunta sobre las derivadas.
Con el uso de la tabla de derivadas k (constante) x f'(x) . La pregunta es : ¿ La k (constante) puede llevar raíz, o elevado a un número o elevado a una fracción o para que sea K(constante) solo tiene que llevar el número y ya está?
-
Hola.
Me podrían explicar como se hacen estas 2 derivadas.
Las tengo que hacer por la tabla general, es decir, K(constante) x f'(x).
Gracias por su atención.
Una pregunta: ¿¿ La K(constante) puede llevar una potencia o elevado a una fracción o llevar una raíz ??
Si me puede hacer un ejemplo si existiera. Si no le importa, gracias.
Le envió la foto: