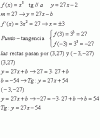-


Antonio Silvio Palmitano
el 3/1/20Vamos con una orientación.
Tienes la ecuación matricial:
A*X*A + 2*B = C*B, restas 2*B en ambos miembros, y queda:
A*X*A = C*B - 2*B, introduces el elemento neutro de la multiplicación de matrices en el último término, y queda:
A*X*A = C*B - 2*I2*B, extraes factor común derecho en el segundo miembro, y queda:
A*X*A = (C - 2*I2)*B, multiplicas por izquierda por la matriz inversa de A en ambos miembros, y queda:
A-1*(A*X*A) = A-1*(C - 2*I2)*B, multiplicas por derecha por la matriz inversa de A en ambos miembros, y queda:
A-1*(A*X*A)*A-1 = A-1*(C - 2*I2)*B*A-1, aplicas la propiedad asociativa de la multiplicación de matrices en el primer miembro, y queda:
(A-1*A)*X*(A*A-1) = A-1*(C - 2*I2)*B*A-1, aplicas la propiedad de existencia del inverso multiplicativo en los agrupamientos del primer miembro, y queda:
I2*X*I2 = A-1*(C - 2*I2)*B*A-1, aplicas la propiedad asociativa en el primer miembro, y queda:
(I2*X)*I2 = A-1*(C - 2*I2)*B*A-1,
aplicas la propiedad de existencia del elemento neutro de la multiplicación de matrices en el agrupamiento del primer miembro, y queda:
X*I2 = A-1*(C - 2*I2)*B*A-1,
aplicas la propiedad de existencia del elemento neutro de la multiplicación en el primer miembro, y queda:
X = A-1*(C - 2*I2)*B*A-1,
y solo queda que calcules la expresión de la matriz inversa de A (observa que A es una matriz cuadrada de orden dos, y que su determinante es distinto de cero), y hagas los cálculos matriciales.
Haz el intento de terminar la tarea, y si te resulta necesario no dudes en volver a consultar.
Espero haberte ayudado.
-
Tengo una superficie de R3 parametrizada de forma que solo depende de una variable (la t). Tengo un punto crítico y necesito saber si es máximo, mínimo o punto de silla. Para ello calculo la Hessiana pero solo tiene una componente (pues la función va a R y tengo una sola variable). Al evaluarlo en mi punto, cómo sé si es máximo, mínimo o punto de silla?
-
Sea T la vida útil (en número de pipetades) de una pipeta electrónica multifuncional de una determinada marca. Supongamosque T es una v.a. continua con densidad de la forma:
fT (x) = 0 si x < 1 0.005/x1.005 si x > 1
a) compramos 15 pipetas de estas. ¿Cuál es la probabilidad de que 13 duren más de 42000 pipetadas?
b) Un técnico usa estas pipetas : cada vez que la que tiene se estropea, compra una nueva. ¿Cuál es la probabilidad
que la primera que le dure más de 42000 pipetades sea la cuarta que compre?
Ayuda por favor !
-
-
Hola.
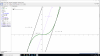
En este problemas que trata sobre adivinar la ecuación general de la recta tangente.
Tengo una duda, porque la pendiente es 27 y -27, eso es lo que no entiendo. Si me lo pudiera explicar, me haría un gran favor.
Muchas gracias por vuestra atención, me ayudáis un montón.
Ahí le envió la foto del ejercicio ya está resuelto.