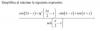-
Saludos, me gustaría resolver una duda sobre un tema básico. Esta expresión (7^3-2)+5-10. A esto se le puede llamar una expresión algebraica (ya que contiene simbologia algebraica y la utilización de ley de signos, o es una expresión aritmética?
-
Buenas, necesito que alguien me eche una mano con el siguiente ejercicio:
1-a) Elige los valores para las variables a,b y c cumpliendo la siguiente igualdad b=a+c y resuelve la ecuación. A que conclusión llegas?
ax^2+bx+c=0
b) Elige los valores para las variables a,b y c cumpliendo la siguiente igualdad a+b+c=0 y resuelve la ecuación. A que conclusión llegas?
ax^2+bx+c=0
Gracias.