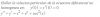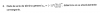-
Hola, por favor me pueden ayudar con este ejercicio de álgebra lineal.
Determine todas las posibilidades para el conjunto soluciones del sistema de ecuaciones lineales que se describe a continuación
a) Un sistema homogéneo de 3 ecuaciones en 5 incógnitas
b) Un sistema homogéneo de 5 ecuaciones en 4 incógnitas
c) Un sistema de 5 ecuaciones en 4 incógnitas
Muchas gracias.
La idea es escribir si tiene infinitas, unica o no tiene solución en cada una de esas y porqué.


Antonius Benedictus
el 14/2/20Sea A la matriz de coeficientes del sistema. Un sistema homogéneo SIEMPRE tiene solución (al menos, la trivial)
a) rango(A)<=3 y 5 incógnitas. Infinitas soluciones.
b) rango(A)<=4. Puede haber solución única o infinitas soluciones.
c) Puede ser cualquier cosa, según sea también la matriz ampliada.
-
-
Que significa que una función escalar de n-variables tenga derivadas parciales continuas en Xo (vector). Es para el estudio de la diferenciabilidad.


Sara
el 31/5/20Hola, mira, me acabo de registrar por que he visto en https://derivadas.es/videos-de-derivadas/ un video de unicoss que es este https://www.youtube.com/watch?v=m_APcwjkup8
Y la verdad es que es bastante útil Alvaro..
Te has mirado esas dos webs ?
Saludos
-
Hola muchachos! En un final que rendi hace unos dias de Analisis matematico, me pidieron resolver la siguiente ecuacion aplicando la Regla de L'Hopital:
lim de x-->0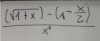
Yo pense que como era una ecuacion racional, podria resolverla a medida que vaya aplicando la regla de y=u/v --> y'=(u'v-uv')/v^2
Pero no, acabe en un loop infinito de seguir aplicando dicha regla y nunca logre quitar esa x del denominador.Agradeceria si me pudieran echar una idea, o al menos decirme donde estoy fallando! Desde ya, muchas gracias.
-

Sebastian Quintero
el 12/2/20Se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis siempre también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro.