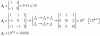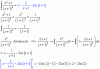-
Hola quiero plantearme la solución particular de una ecuación diferencial, estoy aplicando el método de cauchy euler con el cambio de et=x ; ln(x)=t
este es el ejercicio:
x3y'''-2x2y''-2xy'+8y=ln3(x)+4
después de desarrollar la ecuación mi planteamiento de Yp=At3+B
es correcto? o hay que resolverla por otro método
-
1. En una tienda venden galletas de $ 200= cada una. Se sabe que si una persona compra 1 su costo será una unidad de $ 200=, si la persona compra 2 su costo será lo de 2 unidades de $ 200=, si la persona compra 3 su costo será lo de 3 unidades de $ 200= … en general si la persona compra x unidades su costo será lo de x unidades de $ 200=. Construya la representación algebraica correspondiente, la representación tabular, la representación en diagrama de Venn y la representación en plano cartesiano.
ayuda porfavor


Breaking Vlad
el 12/2/20Se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis siempre también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro.
-

Sebastian Quintero
el 11/2/20se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)