Ya está disponible nuestro nuevo portal donde podrás encontrar nuevas asignaturas, nuevos cursos y nuevas herramientas para ayudarte aún más con tus estudios. Ir a beUnicoos

Incentro de un triangulo

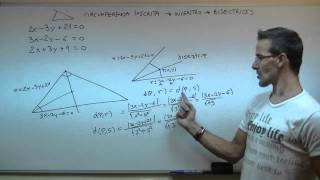
En este ejercicio de GEOMETRIA, dadas las ecuaciones de la recta correspondiente a los lados de un triangulo. deberemos calcular la ecuación de la circunferencia inscrita. Para ello calcularemos la ecuación de dos de las bisectrices igualando distancia de puntos a rectas. Con estas dos ecuaciones obtendremos el incentro (a,b) resolviendo el sistema de dos ecuaciones con dos ingcognitas. El penultimo paso será calcular el radio (distancia del incentro a cualquiera de los lados). Terminaremos hallando la ecuación de la circunferencia con la formula (x-a)²+(y-b)²=R².

Agregar a mi mochila

0/ 1133

* Para utilizar tu mochila o guardar tu progreso y acumular energy points debes ser usuario registrado. Regístrate o inicia sesión

Material adicional

* Los materiales marcados con el símbolo de la estrella () sólo serán accesibles para usuarios PRO. Conviértete en PRO

Foro de preguntas y respuestas

Haz una nueva pregunta * Para dejar preguntas en el foro debes ser usuario registrado. Regístrate o inicia sesión

Manuel Botella Martin
el 21/7/19

hola buenas, siempre he entendido que si tienes un número que este elevado al cuadrado y te da como resultado otro número, se podría resolver quitando ese primer cuadrado y el resultado pasa a ser la raíz cuadrada del mismo resultado, ¿en la ecuación de la circunferencia cabría esa posibilidad?

R²=(X-25)²+(Y-2)² → R=√(X-25)²+(Y-2)²

el resultado sería distinto creo al que sale en el video
65/√13=√(25-25)²+(2-2)²

••0 voto/s
•

Antonius Benedictus
el 21/7/19

El centro de la circunferencia no es un punto de la circunferencia. Por ello, no satisface su ecuación.

•1 voto/s
•

Cancelar
Lautaro Russo
el 31/7/18

Podrías volver a grabar el video?
sería muy guay

••1 voto/s
•

David
el 2/8/18

Tomo nota. Un abrazo!

•0 voto/s
•

Cancelar
José López
el 10/7/18

Tras hacer el ejercicio con las bisectrices internas (y el incentro en (-1,2)) la ecuación de la circunferencia inscrita me da
x²+y²+2x-4y-8=0
Es este resultado el correcto?
Gracias

••0 voto/s
•

Antonius Benedictus
el 10/7/18

Correcto. Te paso mi resolución. Un saludo:

•0 voto/s
•

Cancelar
Elene Altzuguren Arregui
el 16/2/18

Hola! No sé cómo hacer este ejercicio: teniendo las rectas s: 2x + y -1 = 0 ; r: -x = y/7 ; t: (x,y) = (1,3) + α (-1, 1) calcula los vértices del triángulo que forman.
Gracias.

••0 voto/s
•

David
el 26/2/18

Halla el punto de intersección de cada par de rectas. (Toma dos ecuaciones y resuelve el sistema). Toma otras dos y resuelve el sistema... Toma las dos restantes y resuelve el sistema. Besos!

•0 voto/s
•

Cancelar
Doramas Lopez
el 25/5/17

Hola, buenas, ¿si me dan sólo la ecuación general para que saque el vector, el vector que salga será el perpendicular?

••0 voto/s
•

Antonius Benedictus
el 25/5/17

•0 voto/s
•

Cancelar
ale
el 23/3/17

yo por ejemplo, use las rectas s y t y al despejar me quedaron dos ecuaciones tambien, pasé una hacia el otro miembro y se me fue la x, despejé y obtuve y=2, pero luego al sustituir en cualquiera de las rectas me sale x=15/2...

••0 voto/s
•

David
el 17/4/17

Y ¿cual es tu duda?

•0 voto/s
•

Cancelar
molrosales
el 23/4/16

Se me presenta una duda. Cuando deduces la ecuación de la bisectriz igualando las dos fórmulas de distancia del punto al centro...., se presenta un módulo. Por lo tanto habría que considerar las dos posibles soluciones. Es decir, dos rectas que se cortan tienen.. por lo tanto, 2 bisectrices. (que son a su vez perpendiculares). En el problema solo consideras una. ¿Como sabes que la ecuación de bisectriz que va hacia el centro del triangulo es la que consideraste? ¿Y si es la que va hacia fuera? Me parece que la única manera de saberlo es estudiando las pendientes (y por tanto la inclinación) de ambas bisectrices ¿verdad?.
••0 voto/s
•

David
el 24/4/16

Lo aclaro en la descripción del video.. Para hallar la bisectriz para poder obtener el incentro de un triangulo debes tener en cuenta la bisectriz que pasa por la región contenida dentro del triangulo...
•2 voto/s
•

Cancelar
Antonia Pastrana Ayala
el 13/4/16

En el apartado de errores dice que has echo el sistema de encuaciones entre estas ecuaciones 5x+y+3=0 y x-y+3=0, ¿como las calculas ?. Gracias
••0 voto/s
•

David
el 14/4/16

Por reduccion, sumando ambas ecuaciones... 6x+6=0... 6x=-6.. x=-1...
•0 voto/s
•

Cancelar
Marimar Sebastian Diez
el 30/3/16

no hace falta hacer las bisectrices negativas? gracias
••0 voto/s
•

David
el 31/3/16

Te sugiero leas la descripcion del video y el apartado de errores. Besos!
•0 voto/s
•

Cancelar
azul
el 9/7/15

¿CÓMO SE LLAMA EL OTRO VÍDEO? EL QUE MENCIONAS AL PRINCIPIO DE 34'
••0 voto/s
•

David
el 12/7/15

El video anterior a este... #nosvemosenclase ;-)
•1 voto/s
•

Cancelar
Daniel González
el 17/3/15

No entendi lo que dijiste en el minuto 4:16n hablaste muy rapido
¿Ahi en el denominador no va A²+B²+C²?
••0 voto/s
•

David
el 17/3/15

No. Solo A²+B²
•0 voto/s
•

Cancelar
Alexis
el 29/1/15

David tengo una pregunta... empeze a ver el video y con el ejemplo de la primera bisectriz que hicistes me tire yo mismo a hacer la segunda antes de ver como lo hacias tu... y mi resultado fue "-x+5y+15=o" mientras que el tuyo fue "x-15y-15=0" esta mal mi respuesta? Saludos!
••0 voto/s
•

Usuario eliminado
el 29/1/15

Hola Alexis
Lo tienes bien. Es la misma recta
•1 voto/s
•

Cancelar