-


Antonio Silvio Palmitano
el 7/1/20Observa que tienes graficada la componente Ex, y que ésta es positiva (observa que su dirección es horizontal y su sentido es hacia la derecha);
y como tienes que la carga que produce esta componente de campo eléctrico es negativa, observa que el signo negativo en la expresión vectorial (-i) te indica que el punto en estudio, en este caso el origen de coordenadas (O), está ubicado a la izquierda de la carga productora (q1 = -1,6*10-8 C), y que el vector posición del punto en estudio con respecto al punto A donde se encuentra la carga, es:
u = AO = < -3 ; 0 >, cuyo módulo es |u| = 3 m = r1,
y cuyo vector unitario asociado es: U = < -1 ; 0 > = -i.
Luego, tienes que la expresión de la componente que estamos tratando es:
Ex = (k*q1/r12)*U = (9*109*[-1,6*10-8]/32)*(-i) = (-1,6*10)*(-i) = resuelves signos = 16*i N/C.
Espero haberte ayudado.
-
Hola me pueden ayudar con este ejercicio no se si están bien hecho por favor. El vector de posicion de una particula que se mueve en trayectoria circular de radio 0.2cm gira de acuerdo con la ecuacion Θ=(4t^2-6t+8)rad ; el tamaño de la aceleracion total de la particula en t=2s



Antonio Silvio Palmitano
el 6/1/20Tienes la expresión de la función posición angular:
θ(t) = 4*t2 - 6*t + 8 (1) (en radianes);
aquí derivas con respecto al tiempo, y la expresión de la función velocidad angular queda:
ω(t) = 8*t - 6 (2) (en radianes sobre segundo);
aquí derivas con respecto al tiempo, y la expresión de la función aceleración angular queda:
α(t) = 8 (3) (en radianes sobre segundos al cuadrado).
Luego, tienes el radio de la trayectoria:
R = 0,2 cm = 0,002 m.
Luego, evalúas la expresión señalada (2) para el instante en estudio (t = 2s), y queda:
ω(2) = 10 rad/s;
luego, planteas la expresión del módulo de la componente radial de la aceleración, y queda:
aR(2) = R*ω(2)2, reemplazas valores, resuelves, y queda:
aR(2) = 0,002*102, resuelves, y queda:
aR(2) = 0,2 m/s2.
Luego, evalúas la expresión señalada (3) para el instante en estudio (t = 2s), y queda:
α(2) = 8 rad/s2;
luego, planteas la expresión del módulo de la componente tangencial de la aceleración, y queda:
aT(2) = R*α(2), reemplazas valores, y queda:
aT(2) = 0,002*8, resuelves, y queda:
aT(2) = 0,016 m/s2.
Luego, planteas la expresión del módulo de la aceleración total para el instante en estudio, y queda:
a(2) = √[aR(2)2 + aT(2)2], reemplazas los valores de las componentes de la aceleración que tienes remarcados, y queda:
a(2) = √[0,22 + 0,0162], resuelves el argumento de la raíz cuadrada, y queda:
a(2) = √[0,040256] m/s2 ≅ 0,201 m/s2.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 6/1/20Observa que tienes señalada la diagonal del cuadrado, que a su vez es la hipotenusa de los dos triángulos rectángulos isósceles que son sus mitades.
Luego, planteas la longitud de la diagonal señalada, y queda:
r1 = √(r22 + r32) = √([3 m]2 + [3 m]2),
cuyo cuadrado queda expresado:
r12 = [√([3 m]2 + [3 m]2)]2 = [3 m]2 + [3 m]2.
Espero haberte ayudado.
-
Hola, este es un típico problema de física. Dos pelotas de diferente tamaño y masa se dejan caer al mismo tiempo en la Tierra, llegan a la vez? Por que?
Datos:
Mpeq=23,5 +- 0,1g
Mgrand= 26,3 +-0,1g
He leído que la masa no influye en la caída, que solo inflúe la fuerza de rozamiento (si alguien pudiera indicarme la fórmula). Según la explicación que leí, esto se puede observar en que al igualar las dos leyes de Newton (F=ma y F=G·(mM/R^2) SI ALGUIEN PUEDE EXPLICARME POR QUE SE IGUALAN), la masa se iría (¿se podría eliminar la masa en el vacío o en la Tierra también valdría?).
Por lo tanto en este caso debería caer antes el objeto que cuyo rozamiento es menor, en este caso la bola pequeña que es de menor masa.
Sin embargo, en otra página se explicaba que un elefante llegaba antes al suelo que una pluma. En este caso si influye la masa ya que la fuerza de rozamiento del elefante es mayor que la de la pluma.
Alguien me podría explicar el problema y su resolución? No entiendo mucho. Gracias.


Antonio Silvio Palmitano
el 5/1/20Puedes considerar dos situaciones, y en ambas puedes considerar a su vez otras dos.
1°)
La altura desde la cuál caen las pelotas es pequeña:
a)
si consideras la resistencia del aire, entonces aquí puedes considerar que el peso es constante: P = -M*g, y que la fuerza de resistencia viscosa que ejerce el aire es proporcional a la velocidad en cada instante: frd = -β*v (observa que la fuerza de rozamiento tiene sentido opuesto a la velocidad); luego, aplicas la Segunda Ley de Newton, y queda la ecuación (observa que consideramos un sistema de referencia con eje OY vertical, con origen a nivel del suelo, y con sentido positivo hacia arriba, y observa que sustituimos las expresiones de las fuerzas):
-M*g - β*v = M*a (1),
donde el coeficiente β depende de las dimensiones de las pelotas,
y observa que la ecuación señalada (1) es una ecuación diferencial, donde tienes: v = dy/dt, a = d2v/dt2;
b)
si consideras que la resistencia del aire es despreciable, entonces cancelas el término correspondiente a la fuerza de rozamiento dinámico en la ecuación señalada (1), y queda:
-M*g = M*a, aquí divides por M en ambos miembros, y luego despejas:
a = -g,
por lo que tienes que la aceleración de las pelotas es independiente de sus masas y de sus dimensiones.
2°)
La altura desde la cuál caen las pelotas es grande:
a)
si consideras la resistencia del aire, entonces aquí puedes considerar que el peso es constante: P = -G*MT*Mp/r2, y que la fuerza de resistencia viscosa que ejerce el aire es proporcional a la velocidad en cada instante: frd = -β*v (observa que la fuerza de rozamiento tiene sentido opuesto a la velocidad); luego, aplicas la Segunda Ley de Newton, y queda la ecuación (consideramos un sistema de referencia con eje Or radial, con origen en el centro de la Tierra, y con sentido positivo hacia el exterior de la Tierra, y observa que sustituimos las expresiones de las fuerzas):
-G*MT*Mp/r2 - β*v = Mp*a (3),
donde el coeficiente β depende de las dimensiones de las pelotas;
b)
si consideras que la resistencia del aire es despreciable, entonces cancelas el término correspondiente a la fuerza de rozamiento dinámico en la ecuación señalada (1), y queda:
-G*MT*Mp/r2 = Mp*a, aquí divides por Mp en ambos miembros, y luego despejas:
a = -G*MT/r2,
por lo que tienes que la aceleración de las pelotas es independiente de sus masas y de sus dimensiones,
y observa que la ecuación señalada (1) es una ecuación diferencial, donde tienes: v = dr/dt, a = d2r/dt2.
Espero haberte ayudado.
-
 No entiendo esta resolución. ¿Por qué no aplican W=-mΔV? Gracias!! (y perdón por la calidad de la foto)
No entiendo esta resolución. ¿Por qué no aplican W=-mΔV? Gracias!! (y perdón por la calidad de la foto)


Antonio Silvio Palmitano
el 4/1/20Considera un sistema de referencia cartesiano con ejes OX y OY usuales.
Luego, tienes los valores de las masas y los puntos en los cuáles están ubicadas:
M1 = 3 Kg, en el punto A(3,0),
M2 = 5 Kg, en el punto B(0,1).
i)
Tienes el punto en estudio: O(0,0).
Luego, planteas la expresión del vector posición del punto en estudio con respecto al punto A, y queda:
u = AO = < -3 ; 0 > m, cuyo módulo es: |u| = 3 m, y cuyo vector unitario asociado es: U = u/|u| = < -1 ; 0 >;
luego, planteas la expresión del campo gravitatorio producido por la primera masa en el punto en estudio, y queda:
g1 = -(G*M1/|u|2)*U = -(6,674*10-11*3/32)*< -1 ; 0 > ≅ -2,225*10-11*< -1 ; 0 > ≅ < 2,225*10-11 ; 0 > N/Kg (1).
Luego, planteas la expresión del vector posición del punto en estudio con respecto al punto B, y queda:
V = BO = < 0 ; -1 > m, cuyo módulo es: |V| = 1 m, y observa que este vector es unitario;
luego, planteas la expresión del campo gravitatorio producido por la segunda masa en el punto en estudio, y queda:
g2 = -(G*M2/|V|2)*V = -(6,674*10-11*5/12)*< 0 ; -1 > ≅ -33,370*10-11*< 0 ; -1 > ≅ < 0 ; 33,370*10-11 > N/Kg (2).
Luego, planteas la expresión del campo gravitatorio resultante en el punto en estudio, y queda:
gO = g1 + g2, sustituyes las expresiones vectoriales señaladas (1) (2), y queda:
gO = < 2,225*10-11 ; 0 > + < 0 ; 33,370*10-11 >, resuelves la suma vectorial, y queda:
gO = < 2,225*10-11 ; 33,370*10-11 > N/Kg ≅ < 2,225*10-11 ; 3,337*10-10 > N/Kg.
cuyo módulo queda expresado:
|gO| = √([2,225*10-11]2 + [33,370*10-11]2) ≅ 33,444*10-11 N/Kg ≅ 3,344*10-10 N/Kg.
ii)
Observa que la masa M1 es móvil, y que la masa M2 está fija.
Luego, en la situación inicial, planteas la expresión del vector posición del punto A con respecto al punto B, y queda:
w = BA = < 3-0 ; 0-1 > = < 3 ; -1 >, cuyo módulo es: |w| = √(10) m;
luego, planteas la expresión de la energía potencial inicial, y queda:
EPi = -G*M1*M2/|w| = -6,674*10-11*3*5/√(10) ≅ -31,658*10-11 J ≅ -3,166*10-11 J (3).
Luego, en la situación final, planteas la expresión del vector posición del punto C(-3,0) con respecto al punto B, y queda:
p = BC = < -3-0 ; 0-1 > = < -3 ; -1 >, cuyo módulo es: |p| = √(10) m;
luego, planteas la expresión de la energía potencial final, y queda:
EPf = -G*M1*M2/|p| = -6,674*10-11*3*5/√(10) ≅ -31,658*10-11 J ≅ -3,166*10-11 J (4).
Luego, planteas la ecuación trabajo-variación de energía, y queda:
W = EPf - EPi, reemplazas los valores señalados (3) (4), resuelves, y queda:
W = 0,
y observa que los puntos A y C se encuentran a un mismo potencial con respecto a la segunda masa, y recuerda que la diferencia de energía potencial, que hemos señalado EPf - EPi, es igual al producto de la masa móvil por la diferencia de potencial, y de ahí es que consignan la expresión de tu enunciado.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 4/1/20Me parece que no habría inconveniente en que designes con r al radio del planeta, debido a que es el único radio que necesitas para plantear y resolver el problema. De todas formas, sería conveniente que consultes con tus docentes al respecto, a fin de evitar accidentes o malos entendidos.
-


Antonio Silvio Palmitano
el 5/1/20Vamos con una orientación.
Tienes un triángulo equilátero, considera que sus vértices son los puntos (observa que expresamos sus coordenadas en forma fraccionaria): O(0,0), A(1/2,0) y P(1/4,√(3)/4) (te dejo la tarea de plantear las expresiones de las coordenadas del tercer vértice; y considera que la masa: M1 = 10 Kg está ubicada en el punto O, y que la masa M2 = 10 Kg está ubicada en el punto A.
Luego, planteas la expresión del vector posición del vértice P con respecto al vértice O, y queda:
u = OP = < 1/4 ; √(3)/4 > m, cuyo módulo es: |u| = 1/2 m, y cuyo vector unitario asociado es: U = u/|u| = < 1/2 ; √(3)/2 >;
luego, planteas la expresión vectorial del campo gravitatorio producido por la masa M1 en el vértice P, y queda:
g1 = -(G*M1/|u|2)*U (1).
Luego, planteas la expresión del vector posición del vértice P con respecto al vértice A, y queda:
v = AP = < -1/4 ; √(3)/4 > m, cuyo módulo es: |v| = 1/2 m, y cuyo vector unitario asociado es: V = v/|v| = < -1/2 ; √(3)/2 >;
luego, planteas la expresión vectorial del campo gravitatorio producido por la masa M2 en el vértice P, y queda:
g2 = -(G*M1/|v|2)*V (2).
Luego, queda que reemplaces valores y resuelvas las expresiones vectoriales señaladas (1) (2) (observa que una vez hecha esta tarea ya podrás hacer el gráfico correspondiente), y luego plantees y resuelvas la expresión del campo gravitatorio resultante en el vértice P, a partir de la expresión vectorial:
g = g1 + g2.
Espero haberte ayudado.
-
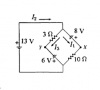
Hola buenas unicoos. Podrían ayudarme a un ejercicio por favor?
. Me pide las Intensidades y la diferencia de potencial en x e y. Lo he planteado pero no sé si está bien planteado ya que este circuito lo encuentro más raro que los otros que he visto.
Mi planteamiento es el siguiente:
I2=I1+I3
13=-8+10I1
13=3I3-6
Y la diferencia de potencial (x-y)=10I1+6
He usado el método de las mallas pero no me queda claro del todo. Espero que puedan ayudarme, muchísimas gracias. Sois los mejores


Antonio Silvio Palmitano
el 5/1/20Has planteado correctamente la Primera Ley de Kirchhoff para el nudo superior, y te ha quedado la ecuación:
I2 = I1 + I3 (1).
Has planteado correctamente la Segunda Ley de Kirchhoff para la malla exterior, y te ha quedado la ecuación:
13 = -8 + 10*I1, aquí sumas 8 en ambos miembros, y queda:
21 = 10*I1, divides por 10 en ambos miembros, y luego despejas:
I1 = 21/10 A = 2,1 A.
Has planteado correctamente la Segunda Ley de Kirchhoff para la malla interior, y te ha quedado la ecuación:
13 = -6 + 3*I3, aquí sumas 6 en ambos miembros, y queda:
19 = 3*I3, divides por 3 en ambos miembros, y luego despejas:
I3 = 19/3 A ≅ 6,333 A.
Luego, reemplazas los valores remarcados en la ecuación señalada (1), y queda:
I2 = 21/10 + 19/3, resuelves, y queda:
I2 = 253/30 A ≅ 8,433 A.
Has planteado correctamente la diferencia de potencial entre el punto x y el punto y, con el tramo inferior de la rama pequeña:
ΔVxy = Vx - Vy, planteas la diferencia de potencial, y queda:
ΔVxy = 10*I1 - (-6) = 10(21/10) + 6 = 21 + 6 = 27 V.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 3/1/20En nuestro planteo vamos a considerar un sistema de referencia con eje OY vertical, con sentido positivo hacia arriba.
Observa que sobre el bloque de plomo están aplicadas dos fuerzas verticales, de las que indicamos sus módulos y sentidos:
Peso: PPb = MPb*g = δPb*VPb*g = δPb*a3*g, hacia abajo;
Acción normal del bloque de madera: N, hacia arriba;
luego, aplicas la Primera Ley de Newton, y queda la ecuación (observa que sustituimos las expresiones de los módulos de las fuerzas):
N - δPb*a3*g = 0, y de aquí despejas: N = δPb*a3*g (1).
Observa que sobre el bloque de madera están aplicadas tres fuerzas verticales, de las que indicamos sus módulos y sentidos:
Peso: PM = MM*g = δM*VM*g, hacia abajo;
Reacción normal del bloque de plomo: N, hacia abajo,
Empuje del agua (observa que este bloque está completamente sumergido): E = δa*VM*g, hacia arriba;
luego, aplicas la Primera Ley de Newton, y queda la ecuación (observa que sustituimos las expresiones de los módulos de las fuerzas):
δa*VM*g - δM*VM*g - N = 0, y de aquí despejas: N = δa*VM*g - δM*VM*g = (δa - δM)*VM*g (2).
Luego, sustituyes la expresión señalada (1) en la ecuación señalada (2), y queda:
δPb*a3*g = (δa - δM)*VM*g, divides por g en todos los términos, y queda:
δPb*a3 = (δa - δM)*VM, divides por x en ambos miembros, y queda:
a3 = (δa - δM)*VM/δPb, extraes raíz cúbica en ambos miembros, y queda:
a = ∛[(δa - δM)*VM/δPb] (3).
Luego, tienes los datos (observa que los expresaremos en unidades internacionales):
δa = 1000 Kg/m3 (densidad del agua),
δM = δMe*δa = 0,61*1000 = 610 Kg/m3 (densidad de la madera),
VM = 60*30*5 = 9000 cm3 = 0,009 m3 (volumen del bloque de madera),
δPb = δPbe*δa = 11,3*1000 = 11300 Kg/m3 (densidad del plomo);
luego, reemplazas datos en la ecuación señalada (3), y queda:
a = ∛[(1000 - 610)*0,009/11300], resuelves, y queda:
a ≅ 0,067724 m ≅ 6,7724 cm.
Espero haberte ayudado.