-
El encunciado es este:
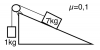
Dado el sistema de la figura. Determina la tensión de la cuerda y la aceleración del sistema sabiendo
que las masas son la izquierda m1 = 1 kg y derecha m2 = 7 kg y el coeficiente de rozamiento es μ = 0,1.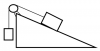
Como no me dan el ángulo no sé hacerlo. -
BUENAS PROFESOR ESTE PROBLEMA COMO SE HACE
Un satélite órbita sobre la superficie de la tierra con una velocidad de 72000m/s . Hallar la altura
Datos : Rt=6370000m go=9,8m/s^2
PERO SOLO CON ESOS DATOS .NO ME DEJA UTILIZAR LA CONSTANTE G
LUEGO ME DICE LA VELOCIDAD DE ESCAPE PARA LLEGAR A ESA ALTURA CALCULARLA
GRACIAS


Antonio Silvio Palmitano
el 16/1/20Si planteas la expresión del módulo del campo gravitatorio terrestre en un punto de la superficie de la Tierra tienes (recuerda que esta expresión es equivalente al módulo de la aceleración gravitatoria terrestre en el punto mencionado):
G*MT/RT2 = g0, y de aquí despejas:
G = g0*RT2/MT,
y luego puedes sustituir esta expresión en lugar de la constante de gravitación universal, en la expresión de la altura orbital del satélite que tienes en el otro desarrollo con el que hemos respondido tu anterior consulta.
De todas maneras, por favor verifica que el enunciado de tu problema esté completo, y también con los datos correctamente consignados.
Espero haberte ayudado.

LOLO HERNANDEZ
el 26/10/21profe tengo una duda , para sacar la fuerza de atraccion que ejerce la gravedad sobre un cuerpo se necesita una constante de gravitacion universal y mi duda es , ¿que es la constante de gravitacion universal? no me refiero a cual es su valor numerico , si no que es en si? un ejemplo, la fuerza normal es la fuerza que ejerce una superficie sobre un cuerpo que es igual a la fuerza que ejerce el cuerpo sobre la superficie , el mismo ejemplo pero con la constante , le pregunto por que no encontre nada similar en internet, todo lo que encontre me daban valor numerico. espero que me pueda responder esa duda. gracias
-
BUENAS PROFESOR ESTE PROBLEMA COMO SE HACE
Un satélite órbita sobre la superficie de la tierra con una velocidad de 72000m/s . Hallar la altura
Datos : Rt=6370000m go=9,8m/s^2


Antonio Silvio Palmitano
el 16/1/20Vamos con una orientación.
Observa que la única fuerza que está aplicada sobre el satélite el la acción gravitatoria que la Tierra ejerce sobre él, por lo que aplicas la Segunda Ley de Newton, y tienes la ecuación (observa que consignamos la expresión del módulo de la fuerza mencionada):
Fg= Ms*aR, sustituyes la expresión del módulo de la fuerza de atracción gravitatoria, y queda:
G*MT*Ms/Ro2 = Ms*aR, divides en ambos miembros por Ms (masa del satélite), y queda:
G*MT/Ro2 = aR, sustituyes la expresión del módulo de la aceleración radial del satélite en función de su rapidez lineal orbital y del radio orbital, y queda:
G*MT/Ro2 = vo2/Ro, multiplicas por Ro2 y divides por vo2 en ambos miembros, y luego despejas:
Ro = G*MT/vo2, sustituyes la expresión del radio orbital del satélite en función del radio terrestre y de la altura orbital, y queda:
RT + ho = G*MT/vo2, restas RT (radio terrestre) en ambos miembros, y queda;
ho = G*MT/vo2 - RT,
que es la expresión de la altura orbital del satélite con respecto a la superficie de la Tierra, en función de la constante gravitacional, de la rapidez lineal orbital del satélite, y de la masa y el radio de la Tierra; luego, solo queda que reemplaces valores y hagas el cálculo.
Espero haberte ayudado.
-
 Tengo dudas en el siguiente problema:
Tengo dudas en el siguiente problema:Un bloque cúbico de madera (densidad específica=0,7gr/cm3) de arista “a” flota en un recipiente con agua. Un bloque de 0,2kg de otro material se sitúa sobre la madera y está se sumerge 2cm más. Determinar la arista “a” del cubo
No se si es que he descompuesto mal las fuerzas, o no sé si he relacionado mal el volumen sumergido del cubo de madera o la densidad del cubo de otro material, pero la arista a me da un número elevado (2345,77cm). Si me pueden explicar en qué he fallado por favor os lo agradecería.


Antonio Silvio Palmitano
el 16/1/20Considera la primera situación con el bloque de madera flotando libremente y parcialmente sumergido en agua:
planteas la expresión del módulo del peso del bloque de madera, y queda:
Pm = Mm*g = δm*Vm*g = δm*a3*g (1);
luego, planteas la la expresión del módulo del empuje que el líquido ejerce sobre el bloque de madera (llamamos h a la longitud de su altura que se encuentra sumergida), y queda:
Em = δa*Vs*g = δa*a2*h*g (2);
luego, establece un sistema de referencia con eje OY vertical con sentido positivo hacia arriba, aplicas la Primera Ley de Newton, y queda la ecuación:
Em - Pm = 0, sumas Pm en ambos miembros, y queda:
Em = Pm, sustituyes las expresiones de los módulos de las fuerzas señaladas (2) (1), y queda:
δa*a2*h*g = δm*a3*g, divides por a2*g en ambos miembros, y queda:
δa*h = δm*a, divides por en ambos miembros, y queda:
h = δm*a/δa (3),
que es la expresión de la altura de la porción sumergida del bloque de madera, en función de la densidad de dicho material, de la arista del bloque cúbico y de la densidad del agua.
Luego, considera la segunda situación, con el nuevo bloque apoyado sobre el bloque de madera:
observa que sobre el bloque de madera están aplicadas tres fuerzas verticales, de las que indicamos sus módulos y sentidos:
Peso: Pm = δm*a3*g, hacia abajo,
Acción normal del nuevo bloque apoyado: N, hacia abajo,
Empuje del líquido: E1 = δa*a2*h1*g,
aplicas la Primera Ley de Newton, y queda la ecuación (observa que sustituimos las expresiones de los módulos de las fuerzas):
δa*a2*h1*g - δm*a3*g - N = 0, sumas N en ambos miembros, y luego despejas:
N = δa*a2*h1*g - δm*a3*g (4);
luego, observa que sobre el nuevo bloque están aplicadas dos fuerzas verticales, de las que indicamos sus módulos y sentidos:
Peso: Pb = Mb*g, hacia abajo,
Reacción del bloque de madera: N, hacia arriba,
aplicas la Primera Ley de Newton, y queda la ecuación (observa que sustituimos la expresión del módulo del peso:
N - Mb*g = 0, sustituyes la expresión señalada (4) en el primer término, y queda:
δa*a2*h1*g - δm*a3*g - Mb*g = 0, divides por g en todos los términos, y queda:
δa*a2*h1 - δm*a3 - Mb = 0, sumas δm*a3 y sumas Mb en ambos miembros, y queda:
δa*a2*h1 = δm*a3 + Mb (5).
Luego, planteas la expresión de la diferencia entre las alturas de las porciones sumergidas, y queda:
h1 - h = Δh, sumas h en ambos miembros, y queda:
h1 = h + Δh (6),
luego, sustituyes la expresión señalada (6) en la ecuación señalada (5), y queda:
δa*a2*(h + Δh) = δm*a3 + Mb, sustituyes la expresión señalada (3) en el primer término del agrupamiento, y queda:
δa*a2*(δm*a/δa + Δh) = δm*a3 + Mb (7).
Luego, tienes los datos (observa que los expresamos en unidades internacionales):
δa = 1000 Kg/m3 (densidad del agua),
δm = 700 Kg/m3 (densidad de la madera),
Δh = 0,02 m (diferencia de alturas de las porciones sumergidas del bloque de madera),
Mb = 0,2 Kg (masa del nuevo bloque apoyado sobre el bloque de madera en las segunda situación);
luego, reemplazas valores en la ecuación señalada (7), resuelves los coeficientes en los términos, y queda:
1000*a2*(0,7*a + 0,02) = 700*a3 + 0,2, distribuyes el primer miembro, y queda:
700*a3 + 20*a2 = 700*a3 + 0,2, restas 700*a3 en ambos miembros, y queda:
20*a2 = 0,2, divides por 20 en ambos miembros, y queda:
a2 = 0,01, extraes raíz cuadrada positiva en ambos miembros, y queda:
a = 0,1 m = 10 cm.
Espero haberte ayudado.
-
Me podríais ayudar con este problema por favor?
Un cuerpo de 10 kg se mueve sobre un plano horizontal en actuar una fuerza de 10 kp paralela al plano. El coeficiente de fricción entre el plano y el cuerpo es de 0,5. calcula: a) Aceleración del movimiento. b) La velocidad después de haber recorrido 10 m. c) El tiempo que tarda en recorrer 10 m.

Antonio Silvio Palmitano
el 16/1/20Establece un sistema de referencia con eje OX paralelo al plano horizontal con dirección y sentido positivo acordes al desplazamiento del cuerpo, cpn ejo OY vertical con sentido positivo hacia arriba, con origen de coordenadas en el punto de partida del cuerpo, con instante inicial: ti = 0 correspondiente a dicha instancia (consideramos que el cuerpo parte desde el reposo).
Luego, planteas la expresión de la función posición y la expresión de la función velocidad de Movimiento Rectilíneo Uniformemente Variado (observa que el cuerpo se desplaza sobre el semieje OX positivo), y queda:
x = xi + vi*t + (1/2)*a*t2,
v = vi + a*t;
luego, reemplazas datos (xi = 0, vi = 0), cancelas términos nulos, y queda:
x = (1/2)*a*t2 (1),
v = a*t (2).
Luego, observa que sobre el cuerpo están aplicadas cuatro fuerzas, de las que indicamos sus módulos, direcciones, y sentidos:
Peso: P = M*g, vertical, negativo,
Acción normal del plano de apoyo: N, vertical, positiva,
Fuerza Externa: F, horizontal, positiva,
Rozamiento dinámico del plano de apoyo: frd = μd*N, horizontal, negativa;
luego, aplicas la Segunda Ley de Newton, y queda (observa que sustituimos las expresiones de los módulos de las fuerzas):
F - μd*N = M*a,
N - M*g = 0, de aquí desepejas: N = M*g (3),
sustituyes la expresión señalada (3) en la primera ecuación, y queda:
F - μd*M*g = M*a (4).
a)
Divides por M en todos los términos de la ecuación señalada (4), y luego despejas:
a = F/M - μd*g, reemplazas valores (F = 10 Kp = 10*9,8 = 98 N, M = 10 Kg, μd = 0,5, g = 9,8 m/s2), resuelves, y queda:
a = 4,9 m/s2.
c)
Reemplazas datos (x = 10 m, a = 4,9 m/s2) en las ecuación señalada (1), resuelves coeficientes, y queda:
10 = 2,45*t2, aquí divides en ambos miembros por 2,45, luego extraes raíz cuadrada positiva en ambos miembros, y queda: t ≅ 2,020 s.
b)
Reemplazas el valor de la aceleración que tienes calculado y el valor del instante en estudio que tienes remarcado en la ecuación señalada (2), y queda:
v ≅ 4,9*2,020, resuelves, y queda:
v ≅ 9,899 m/s.
Espero haberte ayudado.
-
 Tengo dudas en el siguiente problema:
Tengo dudas en el siguiente problema:En un depósito de agua, donde en lo alto del depósito está cerrado, se ejerce una presión manométrica por acción del aire. En una pared lateral, y a 5 metros por debajo del nivel del agua, hay un orificio de 16cm2, en donde el agua sale con una velocidad de 12,5m/s
a) Determinar la presión manométrica en kilopascales (KPa)
b) Calcular los litros que salen del depósito en 3 minutos
No se si los tengo bien resueltos, si me pueden decir si tengo algún fallo y como puedo solucionarlo por favor.
a) La presión manométrica me dio 29,125KPa
b) Los litros de agua que salen en 3 minutos me dio 1200L/min


Antonio Silvio Palmitano
el 16/1/20a)
Has planteado y calculado la presión manométrica.
b)
Planteas la expresión del caudal de agua que fluye por el orificio de salida, y queda:
Q = A*v, reemplazas datos (A = 16 cm2 = 0,0016 m2, v = 12,5 m/s, resuelves, y queda:
Q = 0,02 m3/s = 0,02*1000/(1/60) = 1200 L/min.
Luego, planteas la expresión del volumen de líquido que fluye por el orificio de salida en función del caudal y del intervalo de tiempo correspondiente, y queda:
ΔV = Q*Δt, reemplazas el valor del caudal, y el valor del intervalo de tiempo (Δt = 3 min = 180 s), y queda:
ΔV = 0,02*180, resuelves, y queda:
ΔV = 3,60 m3/s = 3,60*1000/(1/60) = 216000 L/min.
Espero haberte ayudado.
-
Necesito resolver estos ejercicios ya que en febrero tengo la segunda instancia del final y debo aprobar

L


Breaking Vlad
el 15/1/20Se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado, pero no olvidéis de adjuntarlo de forma LITERAL, para saber que os piden. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)


Antonio Silvio Palmitano
el 16/1/207)
Establece un sistema de referencia con origen de coordenadas en la posición del bombero, con eje OX paralelo al segmento d señalado en tu figura con sentido positivo hacia el edificio, y con eje OY vertical con sentido positivo hacia arriba.
Luego, planteas las ecuaciones de posición y de velocidad de Tiro Oblicuo (o Movimiento Parabólico), y queda:
x = xi + vi*senθi*t,
y = yi + vi*senθi*t+ (1/2)*a*t2,
vx = vi*senθi,
vy = vi*senθi + a*t
reemplazas datos iniciales correspondientes a la pequeña porción de chorro de agua que consideras como un móvil (xi = 0, yi = 1 m, θi = 45°, vi = 25 m/s,
a = -g = -9,8 m/s2), resuelves coeficientes, cancelas términos nulos, y queda:
x ≅ 17,678*t (1),
y ≅ 1 + 17,678*t - 4,9*t2 (2),
vx ≅ 17,678 m/s (3),
vy ≅ 17,678 - 9,8*t (4).
a)
Reemplazas las coordenadas del punto de impacto de la masa de agua en el edificio (x = d = 40 m, y = h) en las ecuaciones señaladas (1) (2), y queda:
40 ≅ 17,678*t, de aquí despejas: t ≅ 2,263 s, que es el instante de impacto de la masa de agua en el edificio,
h ≅ 1 + 17,678*t - 4,9*t2 (4);
luego, reemplazas el valor remarcado en los dos últimos términos de la ecuación señalada (4), simplificas, resuelves, y queda:
h ≅ 15,912 m.
b)
Reemplaza el valor del instante de impacto en las expresiones de las componentes de la velocidad de la masa de agua señaladas (3) (4), resuelves, y queda:
vximp ≅ 17,678 m/s,
vyimp ≅ -4,499 m/s;
luego, planteas la expresión del módulo de la velocidad de la masa de agua en el instante de impacto, y queda:
v = √(vximp2 + vyimp2), reemplazas valores, resuelves, y queda:
vimp ≅ 18,242 m/s.
Espero haberte ayudado.


Antonio Silvio Palmitano
el 16/1/209)
Establece un sistema de referencia con origen de coordenadas a nivel del suelo, con eje OY vertical con sentido positivo hacia arriba, con instante inicial: ti = 0 correspondiente al instante en el cuál el tornillo se desprende del ascensor.
Luego, para el ascensor, planteas la ecuación de posición de Movimiento Rectilíneo Uniforme, y queda:
xA = xAi + vA*t, reemplazas datos (xAi = 20 m, vA = 7 m/s), y queda:
xA = 20 + 7* t (1), agregas la ecuación de velocidad del ascensor, y queda:
vA = 7 m/s (2).
Luego, para el tornillo, planteas la ecuación de posición de Movimiento Rectilíneo Uniformemente Variado, y queda:
xT = xTi + vTi*t + (1/2)*aT*t2,
vT = vTi + aT*t, reemplazas datos (xTi = 20 m, vTi = 7 m/s, aT = -g = -9,8 m/s2), resuelves coeficientes, y queda:
xT = 20 + 7*t - 4,9*t2 (3),
vT = 7 - 9,8*t (4).
a)
Planteas la condición de llegada del tornillo a nivel del suelo:
xT = 0, sustituyes la expresión señalada (3) en el primer miembro, y queda:
20 + 7*t - 4,9*t2 = 0, ordenas términos en el primer miembro, multiplicas en todos los términos de la ecuación por -1, y queda:
4,9*t2 - 7*t - 20 = 0, que es una ecuación polinómica cuadrática, cuyas soluciones son:
1°)
t ≅ -1,429 s, que no tiene sentido para este problema,
2°)
t ≅ 2,857 s,
que es el valor del instante en el cuál el tornillo alcanza el nivel del suelo.
b)
Reemplazas este último valor remarcado en la ecuación señalada (4), resuelves, y queda:
vT ≅ -20,999 m/s,
que es la velocidad del tornillo cuando alcanza el nivel del suelo, y observa que el signo negativo indica que su sentido es hacia abajo.
c)
Reemplazas el valor del instante de llegada del tornillo al suelo que tienes remarcado en la ecuación señalada (1), resuelves, y queda:
xA≅ 39,999 m,
que es el valor de la posición del ascensor cuando el tornillo alcanza el nivel del suelo.
Espero haberte ayudado.
-


Breaking Vlad
el 15/1/20Se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado, pero no olvidéis de adjuntarlo de forma LITERAL, para saber que os piden. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)